
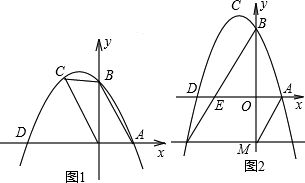
| b |
| 2a |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| OE |
| MN |
| OB |
| MB |
| OE |
| OA |
| BO |
| OM |
| MN |
| BM |
| OA |
| OM |
| -x |
| 4-y |
| 2 |
| -y |
| 8 |
| x+2 |
| 1 |
| 2 |
| 8 |
| x+2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
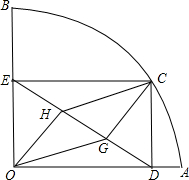 如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是 |
| AB |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
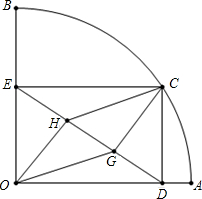 如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是 |
| AB |
 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.
(2013•桥东区二模)如图在Rt△OAB中,∠OAB=90°,OA=AB=6.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届山东济南辛寨乡辛锐中学九年级第三次中考模拟数学试卷(带解析) 题型:解答题
如图,扇形OAB的半径OA=3,圆心角∠AOB=90°,点C是弧AB上异于A、B的动点,过点C作CD⊥OA于点D,作CE⊥OB于点E,连结DE,点G、H在线段DE上,且DG=GH=HE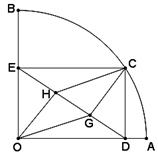
(1)求证:四边形OGCH是平行四边形;
(2)当点C在弧AB上运动时,在CD、CG、DG中,是否存在长度不变的线段?若存在,请求出该线段的长度;
(3)求证: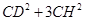 是定值.
是定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com