
ΓΨΧβΡΩΓΩ»γΆΦΘ§…δœΏAMΓΈBNΘ§ΒψEΘ§FΘ§D‘Ύ…δœΏAM…œΘ§ΒψC‘Ύ…δœΏBN…œΘ§«“ΓœBCDΘΫΓœAΘ§BEΤΫΖ÷ΓœABFΘ§BDΤΫΖ÷ΓœFBC.
(1)«σ÷ΛΘΚABΓΈCD.
(2)»γΙϊΤΫ––“ΤΕ·CDΘ§Ρ«Ο¥ΓœAFB”κΓœADBΒΡ±»÷Β «ΖώΖΔ…ζ±δΜ·ΘΩ»τ±δΜ·Θ§’“≥ω±δΜ·Ιφ¬…ΘΜ»τ≤Μ±δΘ§«σ≥ω’βΝΫΗωΫ«ΒΡ±»÷ΒΘ°
(3)»γΙϊΓœAΘΫ100ΓψΘ§Ρ«Ο¥‘ΎΤΫ––“ΤΕ·CDΒΡΙΐ≥Χ÷–Θ§ «Ζώ¥φ‘ΎΡ≥“Μ ±ΩΧΘ§ ΙΓœAEBΘΫΓœBDCΘΩ»τ¥φ‘ΎΘ§«σ≥ω¥Υ ±ΓœAEBΒΡΕ» ΐΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

ΓΨ¥πΑΗΓΩΘ®1Θ©÷ΛΟςΦϊΫβΈωΘΜΘ®2Θ©≤Μ±δ,άμ”…ΦϊΫβΈωΘΜΘ®3Θ©¥φ‘Ύ,60Γψ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΤΫ––œΏΒΡ–‘÷ Θ§“‘ΦΑΒ»ΝΩ¥ζΜΜ÷ΛΟςΓœA+ΓœABC=180ΓψΘ§»ΜΚσΩ…÷ΛΒΟABΓΈCDΘΜ
Θ®2Θ©ΗυΨί»ΐΫ«–ΈΆβΫ«ΒΡ–‘÷ Ω…÷±Ϋ”ΒΟ≥ωΫα¬έΘΜ
Θ®3Θ©ΗυΨίΤΫ––œΏΒΡ–‘÷ ΒΟΒΫΓœABC=80ΓψΘ§…ηΓœCBD=ΓœFBD=ΓœFDB=xΓψΘ§ΗυΨίΫ«ΤΫΖ÷œΏΒΡ–‘÷ ΒΟΒΫΓœEBD=40ΓψΘ§”Ύ «ΒΟΒΫΓœAEB=xΓψ+40ΓψΘ°ΒΟΒΫΓœBDC=80Γψ-xΓψΘ§ΗυΨίΓœAFC=ΓœADBΘ§Ν–ΖΫ≥ΧΦ¥Ω…ΒΟΒΫΫα¬έΘ°
Θ®1Θ©÷ΛΟςΘΚΓΏAMΓΈBNΘ§
ΓύΓœA+ΓœABC=180ΓψΘ§
”÷ΓΏΓœBCD=ΓœAΘ§
ΓύΓœABC+ΓœBCD=180ΓψΘ§
ΓύABΓΈCDΘΜ
Θ®2Θ©ΓΏAMΓΈBNΘ§ΓύΓœADB=ΓœDBCΘ§ΓΏBDΤΫΖ÷ΓœFBCΘ§ΓύΓœFBD=ΓœDBCΘ§
ΓύΓœFBD=ΓœFDBΘ§
Β±CDœρ”“ΤΫ“Τ ±Θ§ΓœFBD‘ω¥σΘ§ΓœABC≤Μ±δΘ§
ΓΏΓœFBD=ΓœFDBΘ§ΓœBFA=ΓœFBD+ΓœFDBΘ§ΓύΓœAFBΘΚΓœADB=2ΘΚ1ΘΜ
Θ®3Θ©¥φ‘ΎΘ§
άμ”…ΘΚΓΏΓœA=100ΓψΘ§ΓύΓœABC=80ΓψΘ§
…ηΓœCBD=ΓœFBD=ΓœFDB=xΓψΘ§
ΓΏBEΤΫΖ÷ΓœABFΘ§BDΤΫΖ÷ΓœFBCΘ§
ΓύΓœEBD=40Γψ
ΓύΓœAEB=xΓψ+40ΓψΘ°
ΓΏAMΓΈBNΘ§ΓœBCD=100ΓψΘ§
ΓύΓœCDA=80ΓψΘ§
ΓύΓœBDC=80Γψ-xΓψΘ§
ΓΏΓœAEB=ΓœBDCΘ§
ΓύxΓψ+40Γψ=80Γψ-xΓψΘ§ΫβΒΟx=20ΓψΘ§
ΓύΓœAEB=20Γψ+40Γψ=60ΓψΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χmx2+3x©¹4=3x2”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυΘ§‘ρmΒΡ÷ΒΩ…“‘ «Θ® Θ©
A.4
B.3
C.2
D.0
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏABΓΔCDœύΫΜ”ΎΒψOΘ§OEΤΫΖ÷ΓœBODΘ°
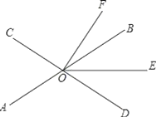
Θ®1Θ©»τΓœAOC=70ΓψΘ§ΓœDOF=90ΓψΘ§«σΓœEOFΒΡΕ» ΐΘΜ
Θ®2Θ©»τOFΤΫΖ÷ΓœCOEΘ§ΓœBOF=15ΓψΘ§»τ…ηΓœAOE=xΓψΘ°
ΔΌ”ΟΚ§xΒΡ¥ζ ΐ Ϋ±μ ΨΓœEOFΘΜ
ΔΎ«σΓœAOCΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
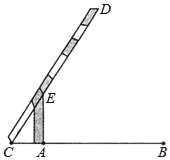
ΓΨΧβΡΩΓΩ»γΆΦΘ§–ΓΟς‘Ύ―–ΨΩ–‘―ßœΑΜνΕ·÷–Θ§Ε‘Ή‘ΦΚΦ“Υυ‘ΎΒΡ–Γ«χΫχ––Βς≤ιΚσΖΔœ÷Θ§–Γ«χΤϊ≥Β»κΩΎΩμABΈΣ3.3mΘ§‘Ύ»κΩΎΒΡ“Μ≤ύΑ≤ΉΑΝΥΆΘ÷ΙΗΥCDΘ§Τδ÷–AEΈΣ÷ßΦήΘ°Β±ΆΘ÷ΙΗΥ―ωΤπ≤Δ”κΒΊΟφ≥…60ΓψΫ« ±Θ§ΆΘ÷ΙΗΥΒΡΕΥΒψC«ΓΚΟ”κΒΊΟφΫ”¥ΞΘ°¥Υ ±CAΈΣ0.7mΘ°‘Ύ¥ΥΉ¥Χ§œ¬Θ§»τ“ΜΝΨΜθ≥ΒΗΏ3mΘ§Ωμ2.5mΘ§»κΩΎΝΫ≤ύ≤ΜΡήΆ®≥ΒΘ§Ρ«Ο¥’βΝΨΜθ≥Β‘Ύ≤Μ≈ωΗΥΒΡ«ιΩωœ¬Θ§Ρή¥”»κΩΎΡΎΆ®Ιΐ¬πΘΩ«κΡψΆ®ΙΐΦΤΥψΥΒΟςΘ°Θ®≤ΈΩΦ ΐΨίΘΚ![]() Γ÷1.7Θ©
Γ÷1.7Θ©
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓœ1+Γœ2=180ΓψΘ§ΓœDAE=ΓœBCFΘ°
Θ®1Θ© ‘≈–Εœ÷±œΏAE”κCF”–‘θ―υΒΡΈΜ÷ΟΙΊœΒΘΩ≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©»τΓœBCF=70ΓψΘ§«σΓœADFΒΡΕ» ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΝβ–ΈABCD÷–Θ§EΘ§FΖ÷±π «ADΘ§BDΒΡ÷–ΒψΘ§»τEF=2Θ§‘ρΝβ–ΈABCDΒΡ÷ή≥Λ « Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§‘ΎΤΫ––ΥΡ±Ώ–ΈABCD÷–Θ§Ν§Ϋ”Ε‘Ϋ«œΏBDΘ§ΉςAEΓΆBD”ΎEΘ§CFΓΆBD”ΎFΘ§ 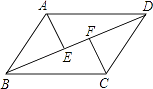
Θ®1Θ©«σ÷ΛΘΚΓςAEDΓ’ΓςCFBΘΜ
Θ®2Θ©»τΓœABC=75ΓψΘ§ΓœADB=30ΓψΘ§AE=3Θ§«σΤΫ––ΥΡ±Ώ–ΈABCDΒΡ÷ή≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΘ®9Ζ÷Θ©»γΆΦΘ§“―÷ΣΒψBΓΔEΓΔCΓΔF‘ΎΆ§“Μ÷±œΏ…œΘ§AB=DEΘ§ΓœA=ΓœDΘ§ACΓΈDFΘ°
«σ÷ΛΘΚΘ®1Θ©ΓςABCΓ’ΓςDEFΘΜ Θ®2Θ©BE=CF
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ(1)ΫΪ“Μ’≈≥ΛΖΫ–Έ÷ΫΤ§Α¥»γΆΦ1Υυ ΨΒΡΖΫ Ϋ’έΒΰΘ§BCΓΔBDΈΣ’έΚέΘ§«σΓœCBDΒΡΕ» ΐΘΜ
(2)ΫΪ“Μ’≈≥ΛΖΫ–Έ÷ΫΤ§Α¥»γΆΦ2Υυ ΨΒΡΖΫ Ϋ’έΒΰΘ§BCΓΔBDΈΣ’έΚέΘ§»τΓœAΓδBEΓδΘΫ50ΓψΘ§«σΓœCBDΒΡΕ» ΐΘΜ
(3)ΫΪ“Μ’≈≥ΛΖΫ–Έ÷ΫΤ§Α¥»γΆΦ3Υυ ΨΒΡΖΫ Ϋ’έΒΰΘ§BCΓΔBDΈΣ’έΚέΘ§»τΓœAΓδBEΓδΘΫΠΝΘ§«κ÷±Ϋ”–¥≥ωΓœCBDΒΡΕ» ΐ(”ΟΚ§ΠΝΒΡ ΫΉ”±μ Ψ)
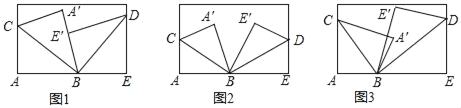
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com