
在△ABC中,AB=AC,∠BAC=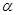 (
(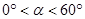 ),将线段BC绕点B逆时针旋转60°得到线段BD。
),将线段BC绕点B逆时针旋转60°得到线段BD。
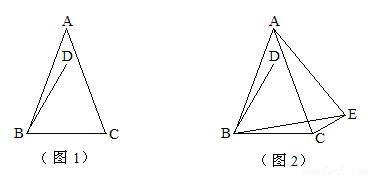
(1)如图1,直接写出∠ABD的大小(用含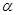 的式子表示);
的式子表示);
(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;
(3)在(2)的条件下,连结DE,若∠DEC=45°,求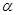 的值。
的值。
(1)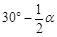 (2)见解析(3)
(2)见解析(3)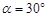
【解析】解:(1)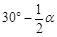 。
。
(2)△ABE为等边三角形。证明如下:
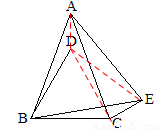
连接AD,CD,ED,
∵线段BC绕点B逆时针旋转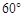 得到线段BD,
得到线段BD,
∴BC=BD,∠DBC=60°。
又∵∠ABE=60°,
∴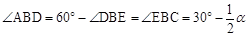 且△BCD为等边三角形。
且△BCD为等边三角形。
在△ABD与△ACD中,∵AB=AC,AD=AD,BD=CD,
∴△ABD≌△ACD(SSS)。∴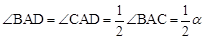 。
。
∵∠BCE=150°,∴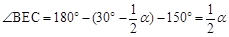 。∴
。∴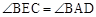 。
。
在△ABD和△EBC中,∵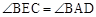 ,
,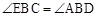 ,BC=BD,
,BC=BD,
∴△ABD≌△EBC(AAS)。∴AB=BE。
∴△ABE为等边三角形。
(3)∵∠BCD=60°,∠BCE=150°,∴ 。
。
又∵∠DEC=45°,∴△DCE为等腰直角三角形。
∴DC=CE=BC。
∵∠BCE=150°,∴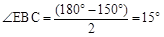 。
。
而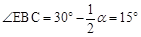 。∴
。∴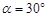 。
。
(1)∵AB=AC,∠BAC=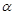 ,∴
,∴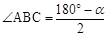 。
。
∵将线段BC绕点B逆时针旋转60°得到线段BD,∴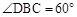 。
。
∴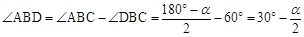 。
。
(2)由SSS证明△ABD≌△ACD,由AAS证明△ABD≌△EBC,即可根据有一个角等于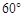 的等腰三角
的等腰三角
形是等边三角形的判定得出结论。
(3)通过证明△DCE为等腰直角三角形得出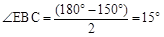 ,由(1)
,由(1)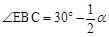 ,从
,从
而 ,解之即可。
,解之即可。


科目:初中数学 来源: 题型:
 (2013•宁德质检)如图,在△ABC中,AB=AC=6,点0为AC的中点,OE⊥AB于点E,OE=
(2013•宁德质检)如图,在△ABC中,AB=AC=6,点0为AC的中点,OE⊥AB于点E,OE=| 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•襄阳)如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.
(2012•襄阳)如图,在△ABC中,AB=AC,AD⊥BC于点D,将△ADC绕点A顺时针旋转,使AC与AB重合,点D落在点E处,AE的延长线交CB的延长线于点M,EB的延长线交AD的延长线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•吉林)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.
(2012•吉林)如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作?ABDE,连接AD,EC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com