
科目:初中数学 来源: 题型:解答题
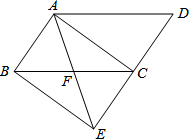 如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.
如图,将?ABCD的边DC延长至点E,使DC=CE,连接AE,交边BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期x | 1 | 2 | 3 | 4 |
| 水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
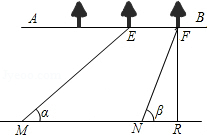 综合实践课,小明所在小组要测量护城河的宽度,如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°.请你根据这些数据帮小明他们算出河宽FR(结果保留整数).
综合实践课,小明所在小组要测量护城河的宽度,如图所示是护城河的一段,两岸AB∥CD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°.请你根据这些数据帮小明他们算出河宽FR(结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 向上攀登的高度x/km | 0.5 | 1.0 | 1.5 | 2.0 |
| 气温y/℃ | 2.0 | -0.9 | -4.1 | -7.0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com