
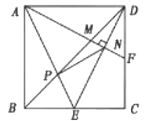
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上的一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则下列结论中:
①![]() ;②
;②![]() ;③tan∠EAF=
;③tan∠EAF=![]() ;④
;④![]() 正确的是()
正确的是()
A. ①②③B. ①②④C. ①③④D. ②③④
【答案】A
【解析】
利用正方形的性质,得出∠DAN=∠EDC,CD=AD,∠C=∠ADF即可判定△ADF≌△DCE(ASA),再证明△ABM∽△FDM,即可解答①;根据题意可知:AF=DE=AE=![]() ,再根据三角函数即可得出③;作PH⊥AN于H.利用平行线的性质求出AH=
,再根据三角函数即可得出③;作PH⊥AN于H.利用平行线的性质求出AH=![]() ,即可解答②;利用相似三角形的判定定理,即可解答④
,即可解答②;利用相似三角形的判定定理,即可解答④
解:∵正方形ABCD的边长为2,点E是BC的中点,
∴AB=BC=CD=AD=2,∠ABC=∠C=∠ADF=90°,CE=BE=1,
∵AF⊥DE,
∴∠DAF+∠ADN=∠ADN+∠CDE=90°,
∴∠DAN=∠EDC,
在△ADF与△DCE中,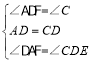 ,
,
∴△ADF≌△DCE(ASA),
∴DF=CE=1,
∵AB∥DF,
∴△ABM∽△FDM,
∴![]() ,
,
∴S△ABM=4S△FDM;故①正确;
根据题意可知:AF=DE=AE=![]() ,
,
∵![]() ×AD×DF=
×AD×DF=![]() ×AF×DN,
×AF×DN,
∴DN=![]() ,
,
∴EN=![]() ,AN=
,AN=![]() ,
,
∴tan∠EAF=![]() ,故③正确,
,故③正确,
作PH⊥AN于H.
∵BE∥AD,
∴![]() ,
,
∴PA=![]() ,
,
∵PH∥EN,
∴![]() ,
,
∴AH=![]() ,
,
∴PH=![]()
∴PN=![]() ,故②正确,
,故②正确,
∵PN≠DN,
∴∠DPN≠∠PDE,
∴△PMN与△DPE不相似,故④错误.
故选:A.


科目:初中数学 来源: 题型:
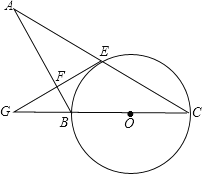
【题目】如图,AB=BC,以BC为直径作⊙O,AC交⊙O于点E,过点E作EG⊥AB于点F,交CB的延长线于点G.
(1)求证:EG是⊙O的切线;
(2)若GF=2![]() ,GB=4,求⊙O的半径.
,GB=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】远远在一个不透明的盒子里装了4个除颜色外其他都相同的小球,其中有3个是红球,1个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某商品的进价为每件40元.现在的售价是每件60元.每星期可卖出300件.市场调查反映:如调整价格,每涨价一元.每星期要少卖出10件;每降价一元,每星期可多卖出18件.如何定价才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
扇形统计图
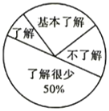
条形统计图

(1)接受问卷调查的学生共有_______人,扇形统计图中“不了解”部分所对应扇形的圆心角度数为_______,并把条形统计图补充完整;
(2)若该中学共有学生![]() 人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为_______人;
(3)若从对校园安全知识达到“了解”程度的![]() ,
,![]() ,
,![]()
![]() 个女生和
个女生和![]() ,
,![]()
![]() 个男生中随机抽取
个男生中随机抽取![]() 人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到
人参加校园安全知识竞赛,请用画树状图法或列表法求出恰好抽到![]() 个男生和
个男生和![]() 个女生的概率.
个女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
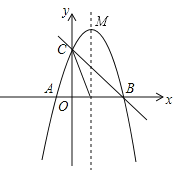
(1)求该抛物线的表达式;
(2)点![]() 是线段
是线段![]() 上方的抛物线上一个动点,求
上方的抛物线上一个动点,求![]() 的面积的最大值;
的面积的最大值;
(3)点![]() 是抛物线的对称轴上一个动点,当以
是抛物线的对称轴上一个动点,当以![]()
![]()
![]() 为顶点的三角形是直角三角形时,求出点
为顶点的三角形是直角三角形时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴相交于点C(0,3),且
轴相交于点C(0,3),且![]() ,
,![]() ,抛物线的顶点为
,抛物线的顶点为![]() .
.
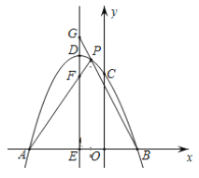
(1)求![]() 、
、![]() 两点的坐标.
两点的坐标.
(2)求抛物线的表达式.
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() ,
,![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),
两点重合),![]() 、
、![]() 与直线
与直线![]() 分别相交于点
分别相交于点![]() 、
、![]() 当点
当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com