练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

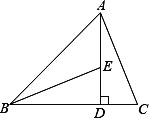
    【题目】已知：如图，在△ABC中，AD⊥BC，交BC于点D，E是线段AD上的点，且AD=BD，DE=DC．

    (1)判断∠BED与∠C的关系，并说明理由.

    (2)若AC=13，DC=5，求AE的长．

    【答案】（1）∠BED=∠C；理由见解析；（2）7.

    【解析】

    （1）可以通过证明△ADC≌△BDE，可得∠BED与∠C的关系；

    （2）首先根据勾股定理，求出AD，由（1）中△ADC≌△BDE，可得ED=EC，AD=BD，即可求出AE.

    （1）∠BED=∠C；

    ∵AD⊥BC

    ∴∠BDE=∠ADC=90°

    又∵在△ADC和△BDE中，

    ∴△ADC≌△BDE（SAS）

    ∴∠BED=∠C

    （2）∵∠ADC=90°，AC=13，DC=5，

    ∴

    又∵△ADC≌△BDE

    ∴DE=DC=5

    ∴AE=AD-DE=12-5=7

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝4，AC＝6，∠ABC和∠ACB的平分线交于O点，过点O作BC的平行线交AB于M点，交AC于N点，则△AMN的周长为（ ）

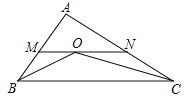
    A. 7 B. 8 C. 9 D. 10

    查看答案和解析>>

    科目：初中数学 来源： 题型：

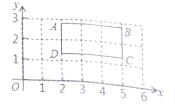
    【题目】长方形放置在如图所示的平面直角坐标系中，点轴，轴，．

    （1）分别写出点的坐标______；______；________．

    （2）在轴上是否存在点，使三角形的面积为长方形ABCD面积的？若存在，请直接写出点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】.中学生带手机上学的现象越来越受到社会的关注，为此某记者随机调查了某市城区若干名中学生家长对这种现象的态度（态度分为：A．无所谓；B．基本赞成；C．赞成；D．反对）．并将调查结果绘制成频数折线统计图1和扇形统计图2（不完整）．请根据图中提供的信息，解答下列问题：

    (1)此次抽样调查中，共调查了 名中学生家长；

    (2)求出图2中扇形C所对的圆心角的度数，并将图1补充完整；

    (3)根据抽样调查结果，请你估计该市城区6000名中学生家长中有多少名家长持反对态度．

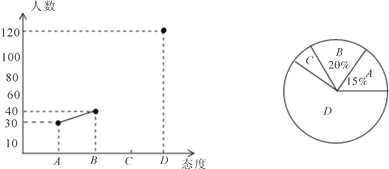
    图1 图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE＝AP＝1，BP＝．下列结论：

    ①△APD≌△AEB；②点B到直线AE的距离为；

    ③S△APD+S△APB＝+；④S正方形ABCD＝4+．

    其中正确结论的序号是_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商城销售A，B两种自行车．A型自行车售价为2 100元/辆，B型自行车售价为1 750元/辆，每辆A型自行车的进价比每辆B型自行车的进价多400元，商城用80 000元购进A型自行车的数量与用64 000元购进B型自行车的数量相等．

    （1）求每辆A，B两种自行车的进价分别是多少？

    （2）现在商城准备一次购进这两种自行车共100辆，设购进A型自行车m辆，这100辆自行车的销售总利润为y元，要求购进B型自行车数量不超过A型自行车数量的2倍，总利润不低于13 000元，求获利最大的方案以及最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

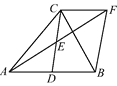
    【题目】如图，在△ABC中，D是AB的中点，E是CD的中点， 过点C作CF//AB交AE的延长线于点F，连接BF．

    (1) 求证：DB＝CF；

    (2) 如果AC＝BC，试判断四边形BDCF的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形纸片ABCD中，AB=3cm，AD=5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．

    （1）求证：四边形BFEP为菱形；

    （2）当点E在AD边上移动时，折痕的端点P、Q也随之移动；

    ①当点Q与点C重合时（如图2），求菱形BFEP的边长；

    ②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“囧”是近时期网络流行语，像一个人脸郁闷的神情如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案阴影部分设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．

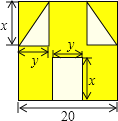
    （1）用含有x、y的代数式表示下图中“囧”的面积；

    （2）当，时，求此时“囧”的面积．

    查看答案和解析>>

    同步练习册答案