Question

9．如图①所示，已知两个边长均为a的全等的正方形ABCD与A₁B₁C₁D₁，正方形ABCD的点C与正方形A₁B₁C₁D₁的中心重合，且绕点C旋转．
（1）当正方形ABCD由图①旋转至图②时，两个阴影部分的面积是否相等？如果相等，直接回答出都等于什么；
（2）当正方形ABCD旋转至任意位置时，如图③，重叠部分的面积会变化吗？说明你的结论．

Answer 1

分析 （1）分别计算图①、图②阴影部分的面积，得出结论；
（2）连接CD₁与CC₁，通过三角形全等，说明图形旋转其阴影面积不变．

解答 解：（1）如图①所示，由于点C与正方形A₁B₁C₁D₁的中心重合，
所以阴影正方形的面积=$\frac{1}{4}$S_{正方形A1B1C1D1}=$\frac{1}{4}$a²；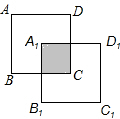
图①
如图②所示，过点C做CE⊥C₁D₁，垂足为E．
由题意易知△D₁CC₁为等腰直角三角形
∴CE=$\frac{1}{2}$a，C₁D₁=a，
∴S_△CC1D1=$\frac{1}{2}$×C₁D₁×CE=$\frac{1}{4}$a²，
∴当正方形ABCD由图①旋转至图②时，两个阴影部分的面积相等，都等于$\frac{1}{4}{a}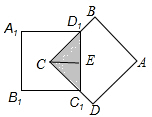^{2}$．
 图②
（2）阴影面积保持不变．理由如下：
如图，连接CD₁、CC₁，
∵正方形ABCD与正方形A₁B₁C₁D₁的边长相等，
∴CD₁=CC₁，∠CD₁E=∠CC₁F=45°，∠ECD=∠D₁CC₁=90°，
∴∠BCD₁+∠D₁CD=∠D₁CD+∠C₁CD=90°，
∴∠BCD₁=∠DCC₁．
在△ECD₁和△FCC₁中，$\left\{\begin{array}{l}{∠BC{D}_{1}=∠FC{C}_{1}}\\{C{D}_{1}=C{C}_{1}}\\{∠C{D}_{1}E=∠C{C}_{1}F}\end{array}\right.$

∴△ECD₁≌△FCC₁
∵C是正方形ABCD的中心，
∴S_阴影=S_△D1CC1=$\frac{1}{4}$S_{正方形A1B1C1D1}=$\frac{1}{4}\\;{a}^{2}$a²．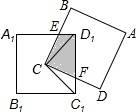
图③
所以阴影面积保持不变．

点评 点评：本题是与正方形中心相关，通过面积计算进行比较和说明的题目．其阴影部分面积不随图形的旋转而变化，运用的是割补的办法，通过三角形全等来说明．