
| A. | $\sqrt{2}$ | B. | $±\sqrt{2}$ | C. | 2 | D. | ±2 |
分析 首先由a2+b2=6ab,即可求得:(a+b)2=8ab,(a-b)2=4ab,然后代入即可求得答案.
解答 解:∵a2+b2=6ab,
∴a2+b2+2ab=8ab,a2+b2-2ab=4ab,
即:(a+b)2=8ab,(a-b)2=4ab,
a+b=±2$\sqrt{2}$$\sqrt{ab}$,a-b=±2$\sqrt{ab}$,
∴当a+b=2$\sqrt{2}$$\sqrt{ab}$,a-b=2$\sqrt{ab}$时,$\frac{a+b}{a-b}$=$\sqrt{2}$;
当a+b=2$\sqrt{2}$$\sqrt{ab}$,a-b=-2$\sqrt{ab}$时,$\frac{a+b}{a-b}$=-$\sqrt{2}$;
当a+b=-2$\sqrt{2}$$\sqrt{ab}$,a-b=2$\sqrt{ab}$时,$\frac{a+b}{a-b}$=-$\sqrt{2}$;
当a+b=-2$\sqrt{2}$$\sqrt{ab}$,a-b=-2$\sqrt{ab}$时,$\frac{a+b}{a-b}$=$\sqrt{2}$.
故选:B.
点评 本题主要考查完全平方公式.注意熟记公式的几个变形公式,还要注意整体思想的应用.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | a2+b2>2ab | B. | a2+b2≥2ab | C. | (a+b)2>2ab | D. | (a+b)2≥2ab |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
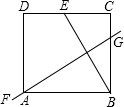 如图,在矩形纸片ABCD中,点E是DC的中点,BE的垂直平分线FG恰好经过点A,则$\frac{BC}{AB}$=( )
如图,在矩形纸片ABCD中,点E是DC的中点,BE的垂直平分线FG恰好经过点A,则$\frac{BC}{AB}$=( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 设上坡路长x千米,可列方程$\frac{x}{3}-\frac{x}{5}=\frac{54}{60}-\frac{42}{60}$ | |
| B. | 设上坡路长x千米,平路长y千米,可列方程组$\left\{\begin{array}{l}\frac{x}{3}+\frac{y}{4}=\frac{54}{60}\\ \frac{x}{5}+\frac{y}{4}=\frac{42}{60}.\end{array}\right.$ | |
| C. | 列算式(54-42)÷(5-3)即可求出上坡路长. | |
| D. | 根据条件,能求出甲地到乙地的全程是3.1千米. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com