
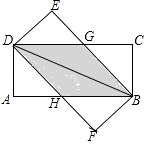
【题目】将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG, 
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
【答案】
(1)解:四边形DHBG是菱形.理由如下:
∵四边形ABCD、FBED是完全相同的矩形,
∴∠A=∠E=90°,AD=ED,AB=EB.
在△DAB和△DEB中, 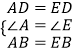 ,
,
∴△DAB≌△DEB(SAS),
∴∠ABD=∠EBD.
∵AB∥CD,DF∥BE,
∴四边形DHBG是平行四边形,∠HDB=∠EBD,
∴∠HDB=∠HBD,
∴DH=BH,
∴DHBG是菱形
(2)解:由(1),设DH=BH=x,则AH=8﹣x,
在Rt△ADH中,AD2+AH2=DH2,即42+(8﹣x)2=x2,
解得:x=5,即BH=5,
∴菱形DHBG的面积为HBAD=5×4=20
【解析】(1)由四边形ABCD、FBED是完全相同的矩形,可得出△DAB≌△DEB(SAS),进而可得出∠ABD=∠EBD,根据矩形的性质可得AB∥CD、DF∥BE,即四边形DHBG是平行四边形,再根据平行线的性质结合∠ABD=∠EBD,即可得出∠HDB=∠HBD,由等角对等边可得出DH=BH,由此即可证出DHBG是菱形;(2)设DH=BH=x,则AH=8﹣x,在Rt△ADH中,利用勾股定理即可得出关于x的一元一次方程,解之即可得出x的值,再根据菱形的面积公式即可求出菱形DHBG的面积.


科目:初中数学 来源: 题型:
【题目】某机动车出发前油箱内有油42L.行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示,根据图象回答问题.
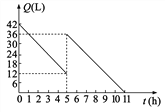
(1)机动车行驶几小时后加油?
(2)中途加油________L;
(3)如果加油站距目的地还有240km,车速为40km/h,要到达目的地,油箱中的油是否够用?并说明原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 我国是世界上严重缺水的国家之一,目前我国年可利用的谈水资源总量为27500亿米3,这个数用科学记数法可表示为( )
A.275×1010B.27.5×1011C.2.75×1012D.2.75×1013
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com