
【题目】如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的![]() ,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )
,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
设正方形B的面积为S,正方形B对角线的交点为O,标注字母并过点O作边的垂线,根据正方形的性质可得OE=OM,∠EOM=90°,再根据同角的余角相等求出∠EOF=∠MON,然后利用“角边角”证明△OEF和△OMN全等,根据全等三角形的面积相等可得阴影部分的面积等于正方形B的面积的![]() ,再求出正方形B的面积=2正方形A的面积,即可得出答案.
,再求出正方形B的面积=2正方形A的面积,即可得出答案.
解:设正方形B对角线的交点为O,如图1,
设正方过点O作边的垂线,则OE=OM,∠EOM=90°,
∵∠EOF+∠EON=90°,∠MON+∠EON=90°,
∴∠EOF=∠MON,
在△OEF和△OMN中
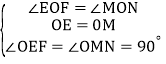 ,
,
∴△OEF≌△OMN(ASA),
∴阴影部分的面积=S四边形NOEP+S△OEF=S四边形NOEP+S△OMN=S四边形MOEP=![]() S正方形CTKW,
S正方形CTKW,
即图1中阴影部分的面积=正方形B的面积的四分之一,
同理图2中阴影部分烦人面积=正方形A的面积的四分之一,
∵图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的![]() ,
,
∴正方形B的面积=正方形A的面积的2倍,
∴图2中重叠部分面积是正方形B面积的![]() ,
,
故选:D.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图角如图3,则下列结论:①abc>0;②a+b+c=2;③a>![]() ;④b<1.其中正确的结论是( )
;④b<1.其中正确的结论是( )

A. ①② B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC≌Rt△EDF,∠ACB=∠F=90°,∠A=∠E=30°.△EDF绕着边AB的中点D旋转, DE,DF分别交线段AC于点M,K.
(1)观察: ①如图2、图3,当∠CDF=0° 或60°时,AM+CK_______MK(填“>”,“<”或“=”).
②如图4,当∠CDF=30° 时,AM+CK___MK(只填“>”或“<”).
(2)猜想:如图1,当0°<∠CDF<60°时,AM+CK_______MK,证明你所得到的结论.
(3)如果![]() ,请直接写出∠CDF的度数和
,请直接写出∠CDF的度数和![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,
边的中点,![]() ,
,![]() 绕
绕![]() 点旋转,它的两边分别交
点旋转,它的两边分别交![]() 和
和![]() (或它们的延长线)于
(或它们的延长线)于![]() ,
,![]() .
.

(1)当![]() 于
于![]() 时(如图1),可得
时(如图1),可得![]() ______________
______________![]() .
.
(2)当![]() 与
与![]() 不垂直时(如图2),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出
不垂直时(如图2),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出![]() ,
,![]() ,
,![]() 的关系.
的关系.
(3)当点![]() 在
在![]() 延长线上时(如图3),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出
延长线上时(如图3),第(1)小题得到的结论成立吗?若成立,请给予证明;若不成立,请直接给出![]() ,
,![]() ,
,![]() 的关系.
的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的解是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①x﹣(3x+1)=﹣5;②![]() +1=0;③3x﹣1=0 中,不等式组
+1=0;③3x﹣1=0 中,不等式组![]() 的关联方程是 (填序号);
的关联方程是 (填序号);
(2)若不等式组![]() 的某个关联方程 2x-m=1 的解是整数, 求 m 的值;
的某个关联方程 2x-m=1 的解是整数, 求 m 的值;
(3)若方程![]() ﹣
﹣![]() x=
x=![]() x,3+x=2(x+
x,3+x=2(x+![]() )都是关于 x 的不等式组
)都是关于 x 的不等式组![]() 的关联方程,直接写出 m的取值范围.
的关联方程,直接写出 m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0).下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(![]() ,y2)是抛物线上两点,则y1>y2.
,y2)是抛物线上两点,则y1>y2.
其中说法正确的是( )
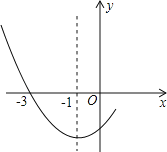
A. ①② B. ②③ C. ①②④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com