
【题目】如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3).
(1)求抛物线的解析式;
(2)D是y轴正半轴上的点,OD=3,在线段BD上任取一点E(不与B,D重合),经过A,B,E三点的圆交直线BC于点F,
①试说明EF是圆的直径;
②判断△AEF的形状,并说明理由.
【答案】解:(1)∵抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于C(0,﹣3),
∴有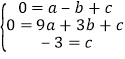 ,解得
,解得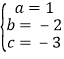 ,
,
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)按照题意画出图形,如下图,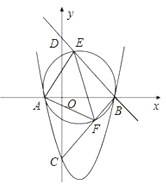
①∵B点坐标(3,0)、C点坐标(0,﹣3),
∴OB=OC=3,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
又∵D是y轴正半轴上的点,OD=3,
∴△BOD为等腰直接三角形,
∴∠OBD=45°,
∠CBD=∠CBO+∠OBD=45°+45°=90°,
即∠FBE=90°,
∴EF是圆的直径.
②∵∠CBO=∠OBD=45°,∠AFE=∠OBD,∠AEF=∠CBO(在同圆中,同弧所对的圆周角相等),
∴∠AEF=∠AFE=45°,
∴∠FAE=90°,AE=AF,
∴△AEF是等腰直角三角形.
【解析】(1)将A、B、C三点坐标代入抛物线方程,即可求得a、b、c的值;
(2)①由B、C、D三点的坐标即可得出∠CBO=∠OBD=45°,从而得出∠EBF=90°,即可得出EF为圆的直径;
②利用同圆内,同弧所对的圆周角相等,可以找到∠AEF=∠AFE=45°,从而得出△AEF是等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,矩形ABCD中,BD=5cm,BC=4cm,E是边AD上一点,且BE = ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF + PG的长为( ).

A. 2.5 cm B. 2.8 cm C. 3 cm D. 3.5 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角的度数是.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
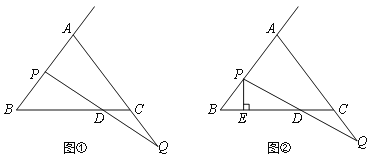
【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
(1)如图,已知等腰直角三角形ABC,∠A=90°,试说明:△ABC是生成三角形;
(2)若等腰三角形DEF有一个内角等于36°,请你画出简图说明△DEF是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为____元/分钟;
(2)买一个篮球需要m元,买一个排球需要n元,则买3个篮球和5个排球共需要____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)0.36+(-7.4)+0.3+(-0.6)+0.64;(2)3![]() +(-2
+(-2![]() )+5
)+5![]() +(-8
+(-8![]() );
);
(3)(-103)+(+1![]() )+(-97)+(+100)+(-1
)+(-97)+(+100)+(-1![]() );
);
(4)(-2![]() )+(-0.38)+(-
)+(-0.38)+(-![]() )+(+0.38);
)+(+0.38);
(5)(-9![]() )+15
)+15![]() +(-3
+(-3![]() )+(-22.5)+(-15
)+(-22.5)+(-15![]() );
);
(6)[(+![]() )+(-3.5)+(-6)]+[(+2.5)+(+6)+(+
)+(-3.5)+(-6)]+[(+2.5)+(+6)+(+![]() )].
)].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com