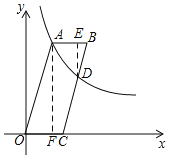
【题目】如图，四边形OABC是平行四边形，点C在x轴上，反比例函数y=
（x＞0）的图象经过点A（5，12），且与边BC交于点D．若AB=BD，则点D的坐标为_____．
【答案】（8， 
）
【解析】解：∵反比例函数
（x＞0）的图象经过点A（5，12），∴k=12×5=60，∴反比例函数的解析式为
，设D（m， 
），由题可得OA的解析式为y=
x，AO∥BC，∴可设BC的解析式为y=
x+b，把D（m， 
）代入，可得
m+b=
，∴b=
﹣
m，∴BC的解析式为y=
x+
﹣
m，令y=0，则x=m﹣
，即OC=m﹣
，∴平行四边形ABCO中，AB=m﹣
，如图所示，过D作DE⊥AB于E，过A作AF⊥OC于F，则△DEB∽△AFO，∴
，而AF=12，DE=12﹣
，OA=
=13，∴DB=13﹣
，∵AB=DB，∴m﹣
=13﹣
，解得m1=5，m2=8，又∵D在A的右侧，即m＞5，∴m=8，∴D的坐标为（8， 
）．故答案为：（8， 
）．
科学实验活动册系列答案科目：初中数学 来源： 题型：
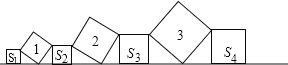
【题目】在直线l上依次摆放着七个正方形，已知斜放置的三个正方形的面积分别为1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则S1+2S2+2S3+S4=________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某移动通讯公司提供了A，B两种方案的通讯费用y(元)与通话时间x(分)之间的关系，如图所示，则以下说法错误的是( )
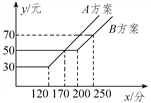
A. 若通话时间少于120分，则A方案比B方案便宜20元
B. 若通话时间超过200分，则B方案比A方案便宜12元
C. 若通讯费用为60元，则B方案比A方案的通话时间多
D. 若两种方案通讯费用相差10元，则通话时间是145分或185分
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y＝k1x＋b与双曲线y＝
相交于点A(1，2)，B(m，－1)两点．
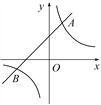
(1)分别求直线和双曲线的表达式；
(2)若A1(x1，y1)，A2(x2，y2)，A3(x3，y3)为双曲线上的三点，且x1<x2<0<x3，请直接写出y1，y2，y3的大小关系．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，△ABC为等边三角形，AQ=PQ，PR=PS，PR⊥AB于R，PS⊥AC于S，现有①点P在∠BAC的平分线上； ②AS=AR；③QP∥AR； ④△BRP≌△QSP四个结论．则对四个结论判断正确的是（ ）
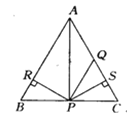
A. 仅①和②正确 B. 仅②③正确 C. 仅①和③正确 D. 全部都正确
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：
甲：9，10，8，5，7，8，10，8，8，7；
乙：5，7，8，7，8，9，7，9，10，10；
丙：7，6，8，5，4，7，6，3，9，5．
（1）根据以上数据完成下表：
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
（2）依据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB＝AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作⊙O的切线DF，交AC于点F．
（1）求证：DF⊥AC；
（2）若⊙O的半径为4，∠CDF＝22.5°，求阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y＝kx＋b与反比例函数y＝
（x＞0）交于A（2，4），B（a，1），与x轴，y轴分别交于点C，D．
（1）直接写出一次函数y＝kx＋b的表达式和反比例函数y＝
（x＞0）的表达式；
（2）求证：AD＝BC．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形ABCD中，对角线AC,BD相交于O点，点P是线段AD上一动点（不与点D重合），PO的延长线交BC于Q点．
（1）求证：四边形PBQD为平行四边形.
（2）若AB=3cm，AD=4cm，P从点A出发．以1cm/s的速度向点D匀速运动．设点P的运动时间为ts，问：四边形PBQD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com