
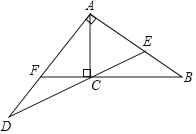
【题目】如图,已知:Rt△ABC中,∠ACB=90°,点E为AB上一点,AC=AE=3,BC=4,过点A作AB的垂线交射线EC于点D,延长BC交AD于点F.
(1)求CF的长;
(2)求∠D的正切值.
【答案】(1)CF=![]() ;(2)tanD=
;(2)tanD=![]() .
.
【解析】
(1)证明△ABC∽△FAC,利用相似三角形的对应边成比例列式求解即可.
(2)过点C作CH⊥AB于点H,由余角的性质可知∠D=∠ECH,先由勾股定理求出AB的长,再根据面积法求出CH的长,再由勾股定理求出AH的长,继而可求出HE的长,然后根据正切的定义求解即可.
(1)∵∠ACB=90°,
∴∠ACF=∠ACB=90°,∠B+∠BAC=90°,
∵AD⊥AB,
∴∠BAC+∠CAF=90°,
∴∠B=∠CAF,
∴△ABC∽△FAC,
∴![]() ,即
,即![]() ,
,
解得CF=![]() ;
;
(2)如图,过点C作CH⊥AB于点H,

∵∠D+∠AED=90°, ∠ECH+∠AED=90°,
∴∠D=∠ECH.
∵AC=3,BC=4,
∴AB=5,
则CH=![]() ,
,
∴AH=![]() =
=![]() ,EH=AE﹣AH=
,EH=AE﹣AH=![]() ,
,
∴tanD=tan∠ECH=![]() .
.


科目:初中数学 来源: 题型:
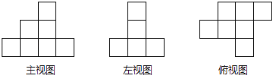
【题目】如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要________个小立方块.最终搭成的长方体的表面积是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
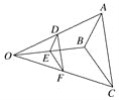
【题目】如图,D,E,F分别是OA,OB,OC的中点,下面的说法中:①△ABC与△DEF是位似图形;②△ABC与△DEF的相似比为1∶2;③△ABC与△DEF的周长之比为2∶1;④△ABC与△DEF的面积之比为4∶1.正确的是( )
A. ①②③ B. ①③④ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )

A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
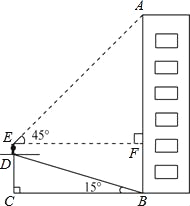
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
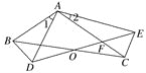
【题目】如图,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC、DE交于点O.则下列四个结论中,①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A、O、C、E四点在同一个圆上,一定成立的有( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com