
如图1,已知双曲线![]() 与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题:
与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题:
(1)若点A的坐标为(4,2),则点B的坐标为 ;当x满足: 时,y1>y2;
(2)过原点O作另一条直线l,交双曲线![]() 于P,Q两点,点P在第一象限,如图2所示.
于P,Q两点,点P在第一象限,如图2所示.
①四边形APBQ一定是 ;
②若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积;
③设点A、P的横坐标分别为m、n,四边形APBQ可能是矩形吗?若可能,求m,n应满足的条件;若不可能,请说明理由.

考点:
反比例函数综合题..
专题:
数形结合.
分析:
数与形相结和,理解正比例函数与反比例函数的性质,并对函数的性质灵活运用,同时也训练了平行四边形和矩形的相关性质.点A与点B关于原点对称,所以B点坐标为(﹣4,﹣2),在第三象限当x<﹣4时y1>y2,在第一象限当0<x<4时y1>y2.由对角线互相平分的四边形是平行四边形可证明APBQ是平行四边形.平行四边形的对角线把它分成四个面积相等的三角形,所以只要求出△AOP的面积,再将其乘以4就可以得到APBQ的面积.根据对角线相等的平行四边形是矩形可知,当mn=k时OP=OA,此时APBQ是矩形.
解答:
解:(1)因为正比例函数与反比例都关于原点成中心对称,所以B点的坐标为B(﹣4,﹣2);
由两个函数都经过点A(4,2),可知双曲线的解析式为y1=,直线的解析式为y2=x,
双曲线在每一象限y随x的增大而减小,直线y随x的增大而增大,
所以当x<﹣4或0<x<4时,y1>y2.
(2)①∵正比例函数与反比例函数都关于原点成中心对称,
∴OA=OB,OP=OQ,根据对角线互相平分的四边形是平行四边形可知APBQ一定是平行四边形.
②∵A点的坐标是(3,1)
∴双曲线为y=,
所以P点坐标为(1,3),
过A作x轴的垂线CD交x轴于C,可得直角梯形OPDC,过P作PD⊥DC,垂足为D,
用直角梯形的面积减去直角三角形的面积可得三角形POA的面积为4,再用4×4得四边形APBQ为16.
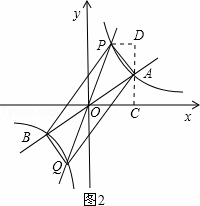
③∵当mn=k时,此时A(m,n),P(n,m),
∴OA=OP,对角线相等且互相平分的四边形是矩形,
∴四边形APBQ是矩形.
点评:
此题考点清晰,难度不大,但数形结合能比较综合的考查学生的分析能力.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:解答题
 与直线y=
与直线y= 交于A,B两点,点A在第一象限,点A的横坐标为4.
交于A,B两点,点A在第一象限,点A的横坐标为4.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
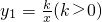 与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题:
与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题: 于P,Q两点,点P在第一象限,如图2所示.
于P,Q两点,点P在第一象限,如图2所示.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
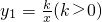 与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题:
与直线y2=k'x交于A,B两点,点A在第一象限.试解答下列问题: 于P,Q两点,点P在第一象限,如图2所示.
于P,Q两点,点P在第一象限,如图2所示.
查看答案和解析>>
科目:初中数学 来源:2014届江苏省无锡市八年级3月月考数学试卷 题型:解答题
如图1,已知双曲线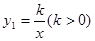 与直线
与直线 交于A,B两点,点A在第一象限.试解答下列问题:
交于A,B两点,点A在第一象限.试解答下列问题:
⑴若点A的坐标为(3,1),则点B的坐标为 ;
⑵当x满足: 时, ;
;
⑶过原点O作另一条直线l,交双曲线 于P,Q两点,点P在第一象限, 如图2所示.
于P,Q两点,点P在第一象限, 如图2所示.
①四边形APBQ一定是 ;
② 若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com