
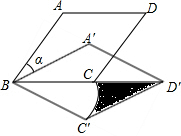
 如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠ABC=60°,把菱形ABCD绕点B顺时针旋转α得到菱形A′BC′D′,其中点D′落在BC的延长线上,点C的运动路径为$\widehat{CC′}$,则图中阴影部分的面积为3$\sqrt{3}$-π.
如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠ABC=60°,把菱形ABCD绕点B顺时针旋转α得到菱形A′BC′D′,其中点D′落在BC的延长线上,点C的运动路径为$\widehat{CC′}$,则图中阴影部分的面积为3$\sqrt{3}$-π. 分析 根据菱形及旋转性质可得∠C′BC=∠A′BA=α=30°、BC′=BC=2$\sqrt{3}$,作C′E⊥BD′于点E,在RT△BC′E中可得BC、C′E的长度,由等腰三角形可知BD′=2BC,最后根据阴影部分面积=S△BC′D′-S扇形CBC′列式计算可得.
解答 解:∵四边形ABCD是菱形,∠ABC=60°,
∴∠A=120°,AB=BC=2$\sqrt{3}$
又∵菱形A′BC′D′是由菱形ABCD绕点B顺时针旋转α得到,
∴∠A′=∠A=120°,A′B=A′D′,∠C′BC=∠A′BA=α,
∴∠C′BC=∠A′BA=α=30°,BC′=BC=2$\sqrt{3}$,
如图,过点C′作C′E⊥BD′于点E,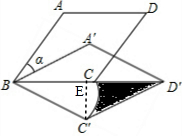
在RT△BC′E中,BE=BC′•cos∠C′BC=2$\sqrt{3}$•$\frac{\sqrt{3}}{2}$=3,
C′E=BC′sin∠C′BC=2$\sqrt{3}$×$\frac{1}{2}$=$\sqrt{3}$,
∴BD′=2BC=6,
则阴影部分面积=S△BC′D′-S扇形CBC′
=$\frac{1}{2}$×6×$\sqrt{3}$-$\frac{30•π•(2\sqrt{3})^{2}}{360}$
=3$\sqrt{3}$-π,
故答案为:3$\sqrt{3}$-π.
点评 本题主要考查了菱形及旋转的性质、扇形面积的计算,根据题意知阴影部分面积=S△BC′D′-S扇形CBC′是解题的根本,熟练根据菱形及旋转性质求得所需线段的长和角的度数是关键.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2016}$ | B. | -$\frac{1}{2016}$ | C. | 2016 | D. | -2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
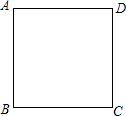 如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.
如图,四边形ABCD为正方形.在边AD上取一点E,连接BE,使∠AEB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 岗位 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 部门A | 部门B | 部门C | 部门D | 部门E |
| 人数 | 1 | 1 | 3 | 1 | 4 | 5 | 12 | 20 | 2 | 1 |
| 月工资数(元) | 15000 | 12000 | 10000 | 9000 | 4000 | 2000 | 1800 | 1500 | 800 | 700 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
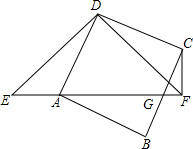 如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.
如图,已知在△EDF中,∠EDF=90°,DE=DF,A是EF上的点,以AD为边作正方形ABCD,它的边BC交EF于G点,连接FC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
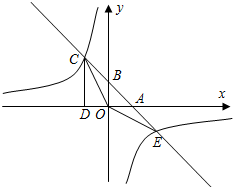 如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$
如图,已知一次函数y=k1x+b的图象分别x轴,y轴交于A、B两点,且与反比例函数y=$\frac{{k}_{2}}{x}$交于C、E两点,点C在第二象限,过点C作CD⊥x轴于点D,OD=1,OE=$\sqrt{10}$,cos∠AOE=$\frac{3\sqrt{10}}{10}$查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.
已知四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,若P为AB边上任意一点,延长PD到E,使DE=2PD,再以PE,PC为边作平行四边形PCQE,则对角线PQ的长的最小值是6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com