
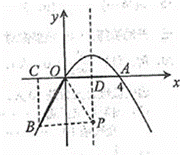
如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A.O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.

考点:二次函数综合题;分类讨论。
解答:解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°,
∵∠AOB=120°,
∴∠BOC=60°,
又∵OA=OB=4,
∴OC=![]() OB=
OB=![]() ×4=2,BC=OB•sin60°=4×
×4=2,BC=OB•sin60°=4×![]() =2
=2![]() ,
,
∴点B的坐标为(﹣2,﹣2![]() );
);
(2)∵抛物线过原点O和点A.B,
∴可设抛物线解析式为y=ax2+bx,
将A(4,0),B(﹣2.﹣2![]() )代入,得
)代入,得
![]() ,
,
解得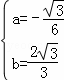 ,
,
∴此抛物线的解析式为y=﹣![]() x2+
x2+![]() x
x
(3)存在,
如图,抛物线的对称轴是x=2,直线x=2与x轴的交点为D,设点P的坐标为(2,y),
①若OB=OP,
则22+|y|2=42,
解得y=±2![]() ,
,
当y=2![]() 时,在Rt△POD中,∠PDO=90°,sin∠POD=
时,在Rt△POD中,∠PDO=90°,sin∠POD=![]() =
=![]() ,
,
∴∠POD=60°,
∴∠POB=∠POD+∠AOB=60°+120°=180°,
即P、O、B三点在同一直线上,
∴y=2![]() 不符合题意,舍去,
不符合题意,舍去,
∴点P的坐标为(2,﹣2![]() )
)
②若OB=PB,则42+|y+2![]() |2=42,
|2=42,
解得y=﹣2![]() ,
,
故点P的坐标为(2,﹣2![]() ),
),
③若OP=BP,则22+|y|2=42+|y+2![]() |2,
|2,
解得y=﹣2![]() ,
,
故点P的坐标为(2,﹣2![]() ),
),
综上所述,符合条件的点P只有一个,其坐标为(2,﹣2![]() ),
),


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
 x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.
x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.查看答案和解析>>
科目:初中数学 来源: 题型:
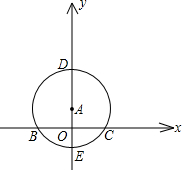
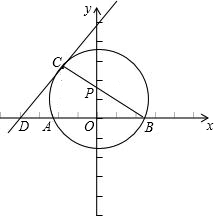 如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于C,过点C的直线y=2x+b交x轴于D,且⊙P的半径为
如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于C,过点C的直线y=2x+b交x轴于D,且⊙P的半径为| 5 |
| k |
| x |
| A、±4 | ||
| B、-4 | ||
C、-2
| ||
| D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
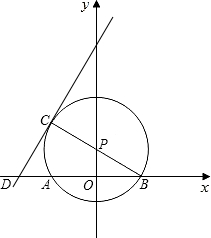 的直线y=2x+b交x轴于D,且⊙P的半径为
的直线y=2x+b交x轴于D,且⊙P的半径为| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 -1)
-1)查看答案和解析>>
科目:初中数学 来源: 题型:
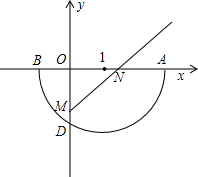 交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.
交于点D,顺次连接I、D、B三点可以组成等边三角形.过A、B两点的抛物线y=ax2+bx+c的顶点P也在半圆I上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com