[题目]中国倡导“一带一路建设将促进我国与世界各国的互利合作.根据规划“一带一路地区覆盖总人口约为44亿人.数据44亿用科学记数法表示为( )A. 44×108 B. 4.4×109 C. 4.4×108 D. 44×1010 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】中国倡导“一带一路”建设将促进我国与世界各国的互利合作，根据规划“一带一路”地区覆盖总人口约为44亿人，数据44亿用科学记数法表示为（　　）

A. 44×108 B. 4.4×109 C. 4.4×108 D. 44×1010

【答案】B

【解析】

用科学记数法表示较大的数时，一般形式为a×10n，其中1≤|a|＜10，n为整数，据此判断即可．

解：44亿=4.4×109；
故选：B．

练习册系列答案

寒假园地青岛出版社系列答案

寒假作业与生活陕西人民教育出版社系列答案

寒假作业陕西旅游出版社系列答案

寒假作业完美假期生活湖南教育出版社系列答案

寒假作业新世界出版社系列答案

宏翔文化快乐学习快乐寒假新疆美术摄影出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】对于正数，用符号表示的整数部分，例如：，，．点在第一象限内，以A为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直. 其中垂直于轴的边长为，垂直于轴的边长为，那么，把这个矩形覆盖的区域叫做点A的矩形域．例如：点的矩形域是一个以为对角线交点，长为3，宽为2的矩形所覆盖的区域，如图1所示，它的面积是6．

图1 图2
根据上面的定义，回答下列问题：
（1）在图2所示的坐标系中画出点的矩形域，该矩形域的面积是；
（2）点的矩形域重叠部分面积为1，求的值；
（3）已知点在直线上，且点B的矩形域的面积满足，那么的取值范围是．（直接写出结果）

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图所示，在平面直角坐标系xOy中，B ， C两点的坐标分别为，，CD⊥y轴于点D ，直线l 经过点D.

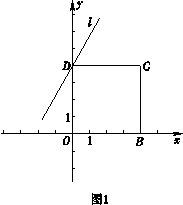
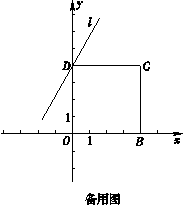
（1）直接写出点D的坐标；
（2）作CE⊥直线l于点E ，将直线CE绕点C逆时针旋转45°，交直线l于点F ，连接BF.
①依题意补全图形；
②通过观察、测量，同学们得到了关于直线BF与直线l的位置关系的猜想，请写出你的猜想；
③通过思考、讨论，同学们形成了证明该猜想的几种思路：
思路1：作CM⊥CF ，交直线l于点M ，可证△CBF≌△CDM ，进而可以得出，从而证明结论.
思路2：作BN⊥CE ，交直线CE于点N ，可证△BCN≌△CDE ，进而证明四边形BFEN为矩形，从而证明结论.
……
请你参考上面的思路完成证明过程.（一种方法即可）