练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．以O为半径的两个同心圆中，大圆的弦AB与CD相等，如果AB与小圆相切
    （1）求证：CD与小圆也相切；
    （2）如果AB=8cm，求这两个圆所形成的圆环面积．

    分析 （1）连接OE，作OF⊥CD于点F，根据等弦所对的弦心距相等，然后根据圆心到直线的距离等于半径，从而证明CD是切线；
    （2）根据S圆环=S大圆-S小圆以及垂径定理、和勾股定理即可求解．

    解答 （1）证明：连接OE，作OF⊥CD于点F．
    ∵AB=CD，
    ∴OF=OE，
    ∴CD与小圆相切；
    （2）解：连接OA．
    S圆环=S大圆-S小圆=πOA2-πOE2=π•OE2=π•AE2=π•（$\frac{AB}{2}$）2=25π．
    故答案是：25；

    点评 本题考查了切线的判定定理和勾股定理，利用切线的性质得到直角三角形，在直角三角形中用勾股定理计算求出大圆的半径．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

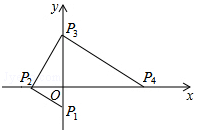    9．如图，点P1，P2，P3，P4均在坐标轴上，且P1P2⊥P2P3，P2P3⊥P3P4，若点P1，P2的坐标分别为（0，-1），（-2，0），求点P4的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：（$\sqrt{2012}$-1）0+（-$\frac{1}{3}$）-1-|$\sqrt{2}$-2|-$\frac{1}{\sqrt{2}+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．已知抛物线y=-$\frac{1}{4}$x2+bx+c与x轴交于A、B，与y轴交于点C，连结AC、BC，D是线段OB上一动点，以CD为一边向右侧作正方形CDEF，连结BF．若C（0，4），B（4，0）且AO=BO．
    （1）求抛物线的解析式；
    （2）求证：BF⊥AB；
    （3）求∠FBE；
    （4）当D点沿x轴正方向移动到点B时，点E也随着运动，则点E所走过的路线长是4$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．已知m-2n=-2，则-3+2m-4n的值为-7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：-5-1
    计算：4.3-（-5）+（-2.3）
    计算：2$\frac{1}{3}$-（+3$\frac{2}{5}$）-（+8$\frac{1}{3}$）+（-8$\frac{3}{5}$）
    计算：（$\frac{3}{8}$+$\frac{1}{6}$-$\frac{3}{4}$）×（-24）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．套用平方差公式计算3×5×（42+1）仿此方法计算：（2+1）（22+1）（24+1）（28+1）…（21024+1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

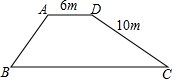    8．如图是一座堤坝的横断面，AB坡坡角为45°，DC坡坡度为1：2，其他数据如图所示，求BC的长（精确到0.1m）．（参考数据：$\sqrt{2}$≈1.414，$\sqrt{5}$≈2.236）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．某市某公交车从起点到终点共有六个站，一辆公交车由起点开往终点，在起点站始发时上了部分乘客，从第二站开始下车、上车的乘客数如表：
    站次
    人数    		二三四五六
    下车（人）3610719
    上车（人）1210940
    （1）求本趟公交车在起点站上车的人数；
    （2）若公交车的收费标准是上车每人2元，计算此趟公交车从起点到终点的总收入？

    查看答案和解析>>

    同步练习册答案