
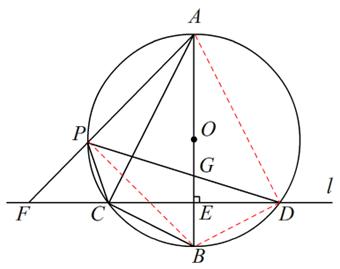
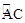 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.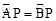 ,求PD的长;
,求PD的长;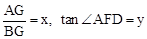 ,求
,求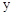 与
与 之间的函数关系式.(不要求写出
之间的函数关系式.(不要求写出 的取值范围)
的取值范围)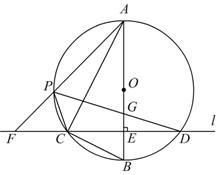
 ;(3)
;(3)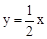 .
.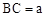 ,应用勾股定理即可求得BC,AC的长,则由AC=2BC得
,应用勾股定理即可求得BC,AC的长,则由AC=2BC得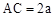 ,由△ACE∽△ABC可求得AE,CE的长,由
,由△ACE∽△ABC可求得AE,CE的长,由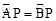 可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得
可知△APB是等腰直角三角形,从而可求得PA的长,由△AEF是等腰直角三角形求得EF=AE=4,从而求得DF的长,由(1)△PAC∽△PDF得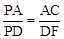 ,即可求得PD的长.
,即可求得PD的长.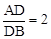 ,由角的转换可得
,由角的转换可得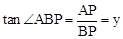 ,由△AGP∽△DGB可得
,由△AGP∽△DGB可得 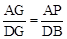 ,由△AGD∽△PGB可得
,由△AGD∽△PGB可得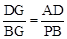 ,两式相乘可得结果.
,两式相乘可得结果.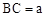 ,∵∠ACB=90°,AB=5,∴
,∵∠ACB=90°,AB=5,∴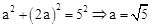 .∴
.∴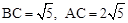 .
.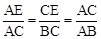 ,即
,即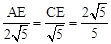 . ∴
. ∴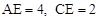 .
.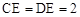 .
.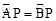 ,∴△APB是等腰直角三角形. ∴∠PAB=45°,
,∴△APB是等腰直角三角形. ∴∠PAB=45°,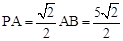 .
.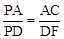 ,即
,即 .
. .
.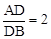 .
.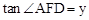 ,∴
,∴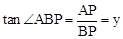 .
.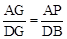 .
.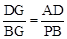 .
.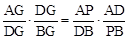 ,即
,即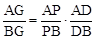 .
.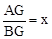 ,∴
,∴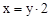 .
.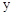 与
与 之间的函数关系式为
之间的函数关系式为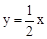 .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com