
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
(1)如图1,当点D在线段BC上时,求证:BD=CF;
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.

【答案】(1)证明见解析;(2)①成立,证明见解析;②GE=2![]() .
.
【解析】试题分析:(1)由SAS证明△DAB≌△FAC,得出对应边相等即可;
(2)①由SAS证明△DAB≌△FAC,得出对应边相等即可;
②过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,证出∠ADH=∠DEM,由AAS证明△ADH≌△DEM,得出EM=DH=6,DM=AH=2,得出CN=EM=6,EN=CM=6,证出△BCG是等腰直角三角形,得出CG=BC=4,求出GN=2,由勾股定理求出GE的长即可.
(1)证明:菱形ADEF中,AD=AF,
∵∠BAC=∠DAF,
∴∠BAD=∠CAF,
在△DAB与△FAC中, 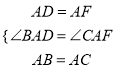 ,
,
∴△DAB≌△FAC(SAS),
∴BD=CF;
(2)解:①(1)中的结论仍然成立;理由如下:
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF
在△DAB与△FAC中, 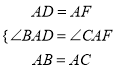 ,
,
∴△DAB≌△FAC(SAS),
∴BD=CF;
②过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,如图所示:
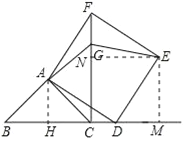
∵∠BAC=90°,AB=AC,
∴BC=![]() AB=4,AH=BH=HC=2,
AB=4,AH=BH=HC=2,
∴CD=BC=4,
∴DH=6,CF=BD=8,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADE=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中, 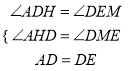 ,
,
∴△ADH≌△DEM(AAS),
∴EM=DH=6,DM=AH=2,
∴CN=EM=6,EN=CM=6,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=2,
∴GE=![]() =
=![]() =2
=2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
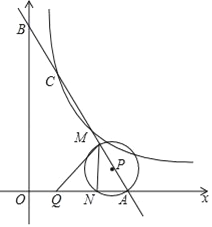
【题目】如图,反比例函数y=![]() (x>0)与一次函数y=kx+6
(x>0)与一次函数y=kx+6![]() 交于点C(2,4
交于点C(2,4![]() ),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
),一次函数图象与两坐标轴分别交于点A和点B,动点P从点A出发,沿AB以每秒1个单位长度的速度向点B运动;同时,动点Q从点O出发,沿OA以相同的速度向点A运动,运动时间为t秒(0<t≤6),以点P为圆心,PA为半径的⊙P与AB交于点M,与OA交于点N,连接MN、MQ.
(1)求m与k的值;
(2)当t为何值时,点Q与点N重合;
(3)若△MNQ的面积为S,试求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】政府为了更好地加强城市建设,就社会热点问题广泛征求市民意见,调查方式是发调查表,要求每位被调查人员只写一个你最关心的有关城市建设的问题,经统计整理,发现对环境保护问题提出的最多,有700人,同时作出相应的条形统计图,如图所示,请回答下列问题.
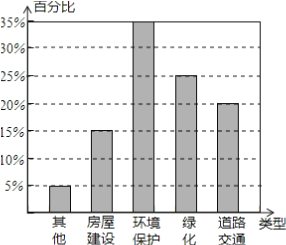
(1)共收回调查表 张;
(2)提道路交通问题的有 人;
(3)请你把这个条形统计图用扇形统计图表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
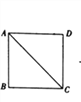
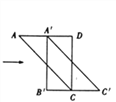
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△![]() ,当两个三角形重叠的面积为32时,则它移动的距离
,当两个三角形重叠的面积为32时,则它移动的距离![]() 等于_____.
等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.
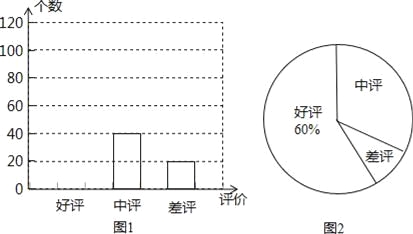
(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列快车从甲地匀速驶往乙地,一列慢车从乙地匀速驶往甲地.设先发车辆行驶的时间为x h,两车之间的距离为y km.当两车均到达各自终点时,运动停止.如图是y与x之间函数关系的部分图象.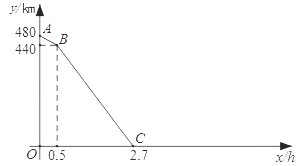
(1)由图象知,慢车的速度为km/h,快车的速度为km/h;
(2)请在图中补全函数图象;
(3)求当x为多少时,两车之间的距离为300km.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com