
【题目】如图,在等边三角形ABC中,BC边上的高AD=6,E是高AD上的一个动点,F是边AB的中点,在点E运动的过程中,存在EB+EF的最小值,则这个最小值是( )
A.3
B.4
C.5
D.6
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx+![]() (a≠0)经过点A(-1,0)和B(3,0).
(a≠0)经过点A(-1,0)和B(3,0).

(1)求抛物线C1的解析式,并写出其顶点C的坐标;
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2,此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标;
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:
①tan∠ENM的值如何变化?请说明理由;
②点M到达点C时,直接写出点P经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校开展的“学习交通安全知识,争做文明中学生”主题活动月中,学校德工处随机选取了该校部分学生,对闯红灯情况进行了一次调查,调查结果有三种情况:A.从不闯红灯;B.偶尔闯红灯;C经常闯红灯.德工处将调查的数据进行了整理,并绘制了尚不完整的统计图如下,请根据相关信息,回答下列问题:
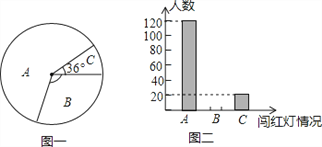
(1)本次活动共调查了_______名学生;
(2)请补全(图二),并求(图一)中 B区域的圆心角的度数_______;
(3)若该校有2400名学生,请估算该校 不严格遵守信号灯指示的有____人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的 ![]() :若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
:若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.6万元,乙队每天的施工费用为5.4万元,工程预算的施工费用为1000万元.若在甲、乙工程队工作效率不变的情况下使施工时间最短,问拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com