Question

8．已知：如图，点A、B分别是∠MON的边OM、ON上两点，OC平分∠MON，在∠CON的内部取一点P（点A、P、B三点不在同一直线上），连接PA、PB．
（1）探索∠APB与∠MON、∠PAO、∠PBO之间的数量关系，并证明你的结论；
（2）设∠OAP=x°，∠OBP=y°，若∠APB的平分线PQ交OC于点Q，求∠OQP的度数（用含有x、y的代数式表示）．

Answer 1

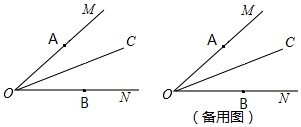
分析 （1）分两种情况进行讨论：点P在直线AB的右侧，点P在直线AB的左侧，分别根据四边形内角和以及三角形外角的性质进行计算即可；
（2）设∠MON=2m°，∠APN=2n°，根据角平分线得出∠AOC=$\frac{1}{2}$∠MON=m°，∠APQ=$\frac{1}{2}$∠APB=n°，再分两种情况，分别根据四边形、三角形的内角和以及三角形外角的性质进行计算，即可得到∠OQP的度数．

解答 解：（1）分两种情况：
①如图1，点P在直线AB的右侧，∠APB+∠MON+∠PAO+∠PBO=360°，
证明：∵四边形AOBP的内角和为（4-2）×180°=360°，
∴∠APB=360°-∠MON-∠PAO-∠PBO；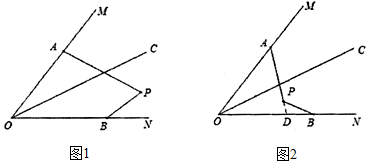

②如图2，点P在直线AB的左侧，∠APB=∠MON+∠PAO+∠PBO，
证明：延长AP交ON于点D，
∵∠ADB是△AOD的外角，
∴∠ADB=∠PAO+∠AOD，
∵∠APB是△PDB的外角，
∴∠APB=∠PDB+∠PBO，
∴∠APB=∠MON+∠PAO+∠PBO；

（2）设∠MON=2m°，∠APN=2n°，
∵OC平分∠MON，
∴∠AOC=$\frac{1}{2}$∠MON=m°，
∵PQ平分∠APB，
∴∠APQ=$\frac{1}{2}$∠APB=n°，
分两种情况：
第一种情况：如图3，∵∠OQP=∠MOC+∠PAO+∠APQ，即∠OQP=m°+x°+n°①
∵∠OQP+∠CON+∠OBP+∠BPQ=360°，
∴∠OQP=360°-∠CON-∠OBP-∠BPQ，即∠OQP=360°-m°-y°-n°②，
①+②得2∠OQP=360°+x°-y°，
∴∠OQP=180°+$\frac{1}{2}$x°-$\frac{1}{2}$y°；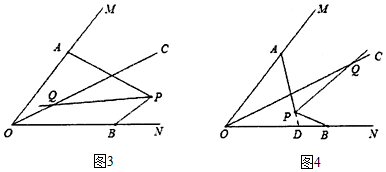

第二种情况：如图4，∵∠OQP+∠APQ=∠MOC+∠PAO，
即∠OQP+n°=m°+x°，
∴2∠OQP+2n°=2m°+2x°①，
∵∠APB=∠MON+∠PAO+∠PBO，
∴2n°=2m°+x°+y°②，
①-②得2∠OQP=x°-y°，
∴∠OQP=$\frac{1}{2}$x°-$\frac{1}{2}$y°，
综上所述，∠OQP=180°+$\frac{1}{2}$x°-$\frac{1}{2}$y°或∠OQP=$\frac{1}{2}$x°-$\frac{1}{2}$y°．

点评 本题主要考查了角的计算以及角平分线的定义的运用，解决问题的关键是掌握四边形内角和、三角形内角和以及三角形外角的性质：三角形的外角等于与它不相邻的两个内角的和．解题时注意分类思想的运用．