
【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=![]() 的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为( )
的图象上,作射线AB,交反比例函数图象于另一点M,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则CM的长度为( )

A. 5 B. 6 C. 4![]() D. 5
D. 5![]()
【答案】D
【解析】
过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,根据直线AB的解析式为y=![]() x+2,可得PF=
x+2,可得PF=![]() ,将△AGP绕点A逆时针旋转90°得△AEH,构造△ADP≌△ADH,再设DE=x,则DH=DP=x+
,将△AGP绕点A逆时针旋转90°得△AEH,构造△ADP≌△ADH,再设DE=x,则DH=DP=x+![]() ,FD=1+2-x=3-x,在Rt△PDF中,根据PF2+DF2=PD2,可得方程(
,FD=1+2-x=3-x,在Rt△PDF中,根据PF2+DF2=PD2,可得方程(![]() )2+(3-x)2=(x+
)2+(3-x)2=(x+![]() )2,解方程求得x=1,即可得D(1,0),再直线AD的解析式为y=3x-3,最后解方程组
)2,解方程求得x=1,即可得D(1,0),再直线AD的解析式为y=3x-3,最后解方程组 求得C点坐标.解方程组
求得C点坐标.解方程组 求得点M的坐标,再根据两点间的距离公式即可求得CM的长.
求得点M的坐标,再根据两点间的距离公式即可求得CM的长.
如图所示,过A作AE⊥x轴于E,以AE为边在AE的左侧作正方形AEFG,交AB于P,

根据点A(2,3)和点B(0,2),可得直线AB的解析式为y=![]() x+2,点A在反比例函数y=
x+2,点A在反比例函数y=![]() 的图象上,可得y=
的图象上,可得y=![]() ,
,
由A(2,3),可得OF=1,
当x=-1时,y=-![]() +2=
+2=![]() ,即P(-1,
,即P(-1,![]() ),
),
∴PF=![]() ,
,
将△AGP绕点A逆时针旋转90°得△AEH,则△ADP≌△ADH,
∴PD=HD,PG=EH=![]() ,
,
设DE=x,则DH=DP=x+![]() ,FD=1+2-x=3-x,
,FD=1+2-x=3-x,
Rt△PDF中,PF2+DF2=PD2,
即(![]() )2+(3-x)2=(x+
)2+(3-x)2=(x+![]() )2,
)2,
解得x=1,
∴OD=2-1=1,即D(1,0),
根据点A(2,3)和点D(1,0),可得直线AD的解析式为y=3x-3,
解方程组 可得
可得![]() 或
或![]()
∴C(-1,-6),
解方程组 可得
可得![]() 或
或![]()
∴M(-6,-1),
∴![]() .
.
故选D.


科目:初中数学 来源: 题型:
【题目】2019年5月26日第5届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )

A. 签约金额逐年增加
B. 与上年相比,2019年的签约金额的增长量最多
C. 签约金额的年增长速度最快的是2016年
D. 2018年的签约金额比2017年降低了22.98%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形![]() 的边长为
的边长为![]() ,将其放置在如图所示的平面直角坐标系中,其中
,将其放置在如图所示的平面直角坐标系中,其中![]() 边在
边在![]() 轴上,
轴上,![]() 边的高
边的高![]() 在
在![]() 轴上.一只电子虫从
轴上.一只电子虫从![]() 出发,先沿
出发,先沿![]() 轴到达
轴到达![]() 点,再沿
点,再沿![]() 到达
到达![]() 点,已知电子虫在
点,已知电子虫在![]() 轴上运动的速度是在
轴上运动的速度是在![]() 上运动速度的
上运动速度的![]() 倍,若电子虫走完全程的时间最短,则点
倍,若电子虫走完全程的时间最短,则点![]() 的坐标为________.
的坐标为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(0,4)、(4,0),点C在第一象限内,∠BAC=90°,AB=2AC,函数y=![]() (x>0)的图象经过点C,将△ABC沿x轴的正方向向右平移m个单位长度,使点A恰好落在函数y=
(x>0)的图象经过点C,将△ABC沿x轴的正方向向右平移m个单位长度,使点A恰好落在函数y=![]() (x>0)的图象上,则m的值为( )
(x>0)的图象上,则m的值为( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,是假命题的是( )
A.在△ABC中,若∠B=∠C﹣∠A,则△ABC是直角三角形
B.在△ABC中,若a![]() =(b+c) (b﹣c),则△ABC是直角三角形
=(b+c) (b﹣c),则△ABC是直角三角形
C.在△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC是直角三角形
D.在△ABC中,若a:b:c=3:4:5,则△ABC是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A在反比例函数y=![]() (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.

查看答案和解析>>
科目:初中数学 来源: 题型:
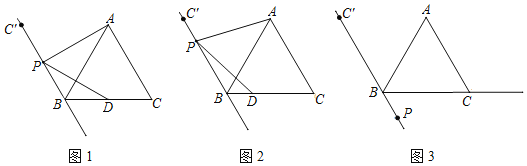
【题目】△ABC是等边三角形,点C关于AB对称的点为C′,点P是直线C′B上的一个动点,连接AP,作∠APD=60°交射线BC于点D.
(1)若点P在线段C′B上(不与点C′,点B重合)
①如图1,当点P是线段C′B的中点时,直接写出线段PD与线段PA的数量关系 .
②如图2,点P是线段C′B上任意一点,证明PD与PA的数量关系.
(2)若点P在线段C′B的延长线上,
①依题意补全图3;
②直接写出线段BD,AB,BP之间的数量关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某生利用标杆测量学校旗杆的高度,标杆CD等于3m,标杆与旗杆的水平距离BD=15m,人的眼睛距地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m.则旗杆AB的高度为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com