
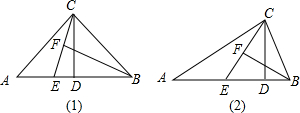
 ��ͼ���ڡ�ABC�У�AB=7��BC=4$\sqrt{2}$����B=45�㣬����P��Qͬʱ��������P��A-C-B�˶����ڱ�AC���ٶ�Ϊÿ��1����λ���ȣ��ڱ�CB���ٶ�Ϊÿ��$\sqrt{2}$����λ���ȣ���Q��B-A-B��ÿ��2����λ���ȵ��ٶ��˶�������һ�����㵽���յ�ʱ����һ������Ҳֹͣ�˶������˶������У�����P��AB�Ĵ�����AB���ڵ�D����PDΪ��������������PDEF������Q��AB�Ĵ���l����������PDEF���ABC�ص�����ͼ�ε����Ϊy��ƽ����λ�����˶�ʱ��Ϊt���룩��
��ͼ���ڡ�ABC�У�AB=7��BC=4$\sqrt{2}$����B=45�㣬����P��Qͬʱ��������P��A-C-B�˶����ڱ�AC���ٶ�Ϊÿ��1����λ���ȣ��ڱ�CB���ٶ�Ϊÿ��$\sqrt{2}$����λ���ȣ���Q��B-A-B��ÿ��2����λ���ȵ��ٶ��˶�������һ�����㵽���յ�ʱ����һ������Ҳֹͣ�˶������˶������У�����P��AB�Ĵ�����AB���ڵ�D����PDΪ��������������PDEF������Q��AB�Ĵ���l����������PDEF���ABC�ص�����ͼ�ε����Ϊy��ƽ����λ�����˶�ʱ��Ϊt���룩������ ��1������P��PD��ֱAB������ΪD���������֪����PDBΪ����ֱ�������Σ��Ӷ������PD�ij���
��2�������AD�ij���Ȼ�����ݹ��ɶ��������AC�ij�����������Ǻ����Ķ���AD=$\frac{3}{5}$t������Q��A��Bʱ��AQ=2��t-3.5����Ȼ����AQ=AD�з�����⼴�ɣ���ͼ2��ʾ������Q��B��Aʱ��AP=t����AD=$\frac{3}{5}$t��BQ=2t����AD+BQ=7�з�����⼴�ɣ�
��3����ͼ4��ʾ���ɷ�Ϊ������ȫ���ڡ�ABC���ڲ��������ε�һ�����ڡ�ABC�ڲ��������ε�һ���ڡ�ABC���ڲ�����������м��㣻
��4�����߶δ�ֱƽ���ߵ����ʿ�֪lΪDE�Ĵ�ֱƽ���ߣ�Ȼ���ú�t��ʽ�ӱ�ʾ��AQ��BQ�ij�������з�����⼴�ɣ�
��� �⣺��1����ͼ1��ʾ��
��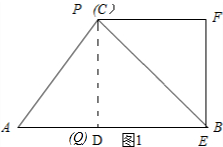
��PD��AB��
���PDB=90�㣮
�֡ߡ�DBP=45�㣮
��PD=BD=BC��$\frac{\sqrt{2}}{2}$=4$\sqrt{2}$��$\frac{\sqrt{2}}{2}$=4��
�ʴ�Ϊ��4��
��2����ͼ1��ʾ����AB=7��BD=4��
��AD=3��
��AC=5��
��sin��A=$\frac{4}{5}$��cos��A=$\frac{3}{5}$��
��ͼ2��ʾ������P��AC��ʱ��AP=t����PD=$\frac{4}{5}$t��AD=$\frac{3}{5}$t��BQ=2t��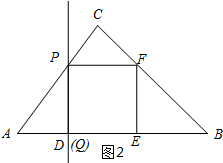
��AD+BQ=7��
��$\frac{3}{5}$t+2t=7��
��ã�t=$\frac{35}{13}$��
��ͼ3��ʾ������Q��A��Bʱ��AD=$\frac{3}{5}$t��AQ=2��t-3.5����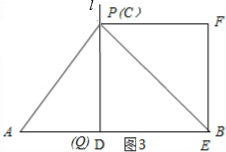
��������ã�$\frac{3}{5}$t=2��t-3.5����
���t=5��
������������t=$\frac{35}{13}$��t=5ʱ����D��ֱ��l�ϣ�
��3����ͼ4��ʾ��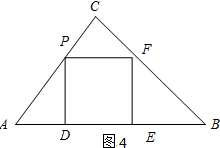
��PD=$\frac{4}{5}$t��
��y=DP2=��$\frac{4}{5}$t��2=$\frac{16}{25}$t2��
����Fǡ����BC��ʱ��EF=BB=$\frac{4}{5}$t��
��AD+DE+EB=7��
��$\frac{3}{5}$t+$\frac{4}{5}$t+$\frac{4}{5}$t=7��
��ã�t=$\frac{35}{11}$��
�൱0��t��$\frac{35}{11}$ʱ��S=$\frac{16}{25}$t2��
��$\frac{35}{11}$��t��5ʱ����ͼ5��ʾ��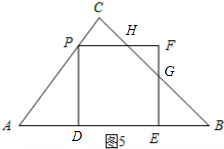
��AQ=$\frac{3}{5}$t��DE=PD=$\frac{4}{5}$t��
��EB=7-$\frac{7}{5}$t��
�ߡ�GEB=90�㣬��B=45�㣬
��EG=EB=7-$\frac{7}{5}$t��
��FG=FE-GE=$\frac{11}{5}$t-7��
��y=PD2-$\frac{1}{2}$FH•FG=-$\frac{89}{50}$t2+$\frac{77}{5}$t-$\frac{49}{2}$��
��5��t��7ʱ����ͼ6��ʾ��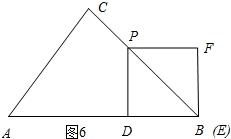
��AD=AC��$\frac{3}{5}$+$\frac{\sqrt{2}}{2}$CP=3+��t-5��=t-2��
��DB=7-��t-2��=9-t��
��y=$\frac{1}{2}$��9-t��2=$\frac{1}{2}$t2-9t+$\frac{81}{2}$��
����������y��t�Ĺ�ϵʽΪS=$\left\{\begin{array}{l}{\frac{16}{25}{t}^{2}��0��t��\frac{35}{11}��}\\{-\frac{89}{50}{t}^{2}+\frac{77}{5}t-\frac{49}{2}��\frac{35}{11}��t��5��}\\{\frac{1}{2}{t}^{2}-9t+\frac{81}{2}��5��t��7��}\end{array}\right.$��
��4����ͼ7��ʾ����lΪDE�Ĵ�ֱƽ����ʱ��ֱ��l������һ��H��ʹ��HD=HE��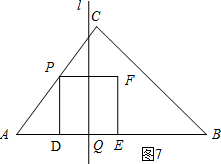
��AD=$\frac{3}{5}$t��DE=DP=$\frac{4}{5}$t��
��AQ=$\frac{3}{5}$t+$\frac{2}{5}$t��
��QB=2t��
��t+2t=7��
��ã�t=$\frac{7}{3}$��
��ͼ8��ʾ��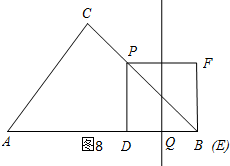
���ɣ�3����֪AD=t-2��PD=9-t��
��AQ=t-2+4.5-$\frac{1}{2}$t=2.5+$\frac{1}{2}$t��
��2.5+$\frac{1}{2}$t=2t-7��
��ã�t=$\frac{19}{3}$��
������������t=$\frac{7}{3}$��t=$\frac{19}{3}$ʱ����ֱ��l�ϴ��ڵ�Hʹ��HD=HE��
���� ������Ҫ��������ı��ε��ۺ�Ӧ�ã��������ҪӦ���������ε����ʡ�����ֱ�������ε����ʣ�����������Ǻ���ֵ��������Ǻ����Ķ��壬�������⻭��ͼ�Σ����ú�t��ʽ�ӱ�ʾ����߶εij����ǽ���Ĺؼ���


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ���Ĵ�ʡ�ɶ��н����ذ��꼶��ѧ����ĩ������ѧ�Ծ��ͣ������棩 ���ͣ������
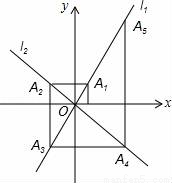
��ͼ����ƽ��ֱ������ϵ�У�����y=2x��y=��x��ͼ��ֱ�Ϊֱ��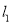 ��
�� 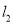 �����㣨1��0����x��Ĵ��߽�
�����㣨1��0����x��Ĵ��߽�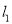 �ڵ�A1������A1��y��Ĵ��߽�
�ڵ�A1������A1��y��Ĵ��߽�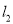 �ڵ�A2������A2��x��Ĵ��߽�
�ڵ�A2������A2��x��Ĵ��߽�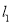 �ڵ�A3������A3��y��Ĵ��߽�
�ڵ�A3������A3��y��Ĵ��߽�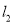 �ڵ�A4�������ν�����ȥ�����A2015������Ϊ__��
�ڵ�A4�������ν�����ȥ�����A2015������Ϊ__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ���Ĵ�ʡ�ɶ��н����ذ��꼶��ѧ����ĩ������ѧ�Ծ��ͣ������棩 ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=-x+b��ͼ��������������y=kx��ͼ������B��3��1��
��1����һ�κ����������������ı���ʽ��
(2����ֱ��CD������������y=kxƽ��,�ҹ���C��0��-4������ֱ��AB�ཻ�ڵ�D�����D������.��ע����ֱ��ƽ�У�  ��ȣ�
��ȣ�
��3������CB����������BCD�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
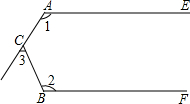 ��ͼ��ֱ��l1��l2����1=110�㣬��2=130�㣬��ô��3�Ķ����ǣ�������
��ͼ��ֱ��l1��l2����1=110�㣬��2=130�㣬��ô��3�Ķ����ǣ�������| A�� | 40�� | B�� | 50�� | C�� | 60�� | D�� | 70�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a+3����a-4�� | B�� | ��a-3����a+4�� | C�� | ��a+6����a-2�� | D�� | ��a-6����a+2�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com