
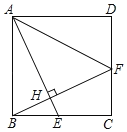
【题目】如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BH⊥AE,垂足为点H,延长BH交CD于点F,连接AF.
(1)求证:AE=BF;
(2)若正方形边长为5,BE=2,求sin∠DAF的值.
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() 与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
与x轴交于A、B两点,△ABC为等边三角形,∠COD=60°,且OD=OC.
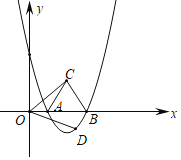
(1)A点坐标为 ,B点坐标为 ;
(2)求证:点D在抛物线上;
(3)点M在抛物线的对称轴上,点N在抛物线上,若以M、N、O、D为顶点的四边形为平行四边形,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
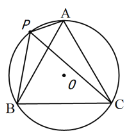
【题目】如图,A、P、B、C是⊙O上四点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形;
(2)连接OA,OB,当点P位于什么位置时,四边形PBOA是菱形?并说明理由;
(3)已知PA=a,PB=b,求PC的长(用含a和b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(m﹣2)x2+2mx+m﹣3的图象与x轴有两个交点,(x1,0),(x2,0),则下列说法正确是( )
①该函数图象一定过定点(﹣1,﹣5);
②若该函数图象开口向下,则m的取值范围为:![]() m<2;
m<2;
③当m>2,且1≤x≤2时,y的最大值为:4m﹣5;
④当m>2,且该函数图象与x轴两交点的横坐标x1,x2满足﹣3<x1<﹣2,﹣1<x2<0时,m的取值范围为:![]() m<11.
m<11.
A.①②③④B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为![]() 米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)
米,点A、D、E在同一水平直线上,则A、B两点间的距离是_____米.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
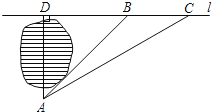
【题目】如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l.小明测量出∠ACD=31°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据 tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系内,正方形如图摆放,已知顶点 A(a,0),B(0,b) ,则顶点C的坐标为( )
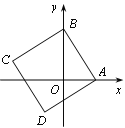
A.(-b,a b)B.(-b,b - a)C.(-a,b - a)D.(b,b -a)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于x的二次函数y=ax2﹣2ax(a>0)的顶点为C,与x轴交于点O、A,关于x的一次函数y=﹣ax(a>0).
(1)试说明点C在一次函数的图象上;
(2)若两个点(k,y1)、(k+2,y2)(k≠0,±2)都在二次函数的图象上,是否存在整数k,满足![]() ?如果存在,请求出k的值;如果不存在,请说明理由;
?如果存在,请求出k的值;如果不存在,请说明理由;
(3)若点E是二次函数图象上一动点,E点的横坐标是n,且﹣1≤n≤1,过点E作y轴的平行线,与一次函数图象交于点F,当0<a≤2时,求线段EF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年在法国举办的女足世界杯,为人们奉献了一场足球盛宴.某商场销售一批足球文化衫,已知该文化衫的进价为每件40元,当售价为每件60元时,每个月可售出100件.根据市场行情,现决定涨价销售,调査表明,每件商品的售价每上涨1元,每个月会少售出2件,设每件商品的售价为![]() 元,每个月的销量为
元,每个月的销量为![]() 件.
件.
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当每件商品的售价定为多少元时,每个月获得利润最大?最大月利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com