
分析 根据根与系数的关系得到x1+x2=$\frac{6(3k-1)}{{k}^{2}-1}$,x1x2=$\frac{72}{{k}^{2}-1}$,则(x1-1)(x2-1)=4得到x1x2-(x1+x2)+1=4,即$\frac{72}{{k}^{2}-1}$-$\frac{6(3k-1)}{{k}^{2}-1}$+1=4,解得k1=-9,k2=3,然后利用x1和x2是两个正根可判断k=3.
解答 解:根据题意得x1+x2=$\frac{6(3k-1)}{{k}^{2}-1}$,x1x2=$\frac{72}{{k}^{2}-1}$,
∵(x1-1)(x2-1)=4,
∴x1x2-(x1+x2)+1=4,
∴$\frac{72}{{k}^{2}-1}$-$\frac{6(3k-1)}{{k}^{2}-1}$+1=4,
整理得k2+6k-27=0,解得k1=-9,k2=3,
经检验k1=-9,k2=3是分式方程的解,
∵x1和x2是两个正根,
∴x1+x2=$\frac{6(3k-1)}{{k}^{2}-1}$>0,x1x2=$\frac{72}{{k}^{2}-1}$>0,
∴k的值为3.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.也考查了解分式方程.


科目:初中数学 来源: 题型:选择题
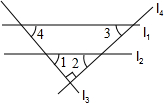 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )| A. | 只有①正确 | B. | 只有②正确 | C. | ①和③正确 | D. | ①②③都正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )
小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )| A. | (60+x)(40+x)×54%=60×40 | B. | (60+2x)(40+2x)×54%=60×40 | ||
| C. | (60+2x)(40+2x)=60×40×54% | D. | (60+x)(40+x)=60×40×54% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 60° | 72° | 90° | 120° |
| R关于r的函数解析式 | 6r | 5r | 4r | 3r |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com