
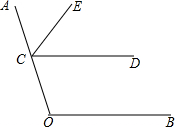
 ��ͼ����C������OA�ϣ�CEƽ�֡�ACD��OFƽ�֡�COB��������CD���ڵ�F��
��ͼ����C������OA�ϣ�CEƽ�֡�ACD��OFƽ�֡�COB��������CD���ڵ�F������ ��1���������ⲹȫͼ�μ��ɣ�
��2�����ݽ�ƽ���ߵĶ���õ���ACE=$\frac{1}{2}$��ACD����COF=$\frac{1}{2}$��COB������ͬ�ǵIJ�����ȵõ���ACE=��COF��
���  �⣺��1����ȫͼ�Σ���ͼ��ʾ��
�⣺��1����ȫͼ�Σ���ͼ��ʾ��
��2��֤������CEƽ�֡�ACD��OFƽ�֡�COB��
���ACE=$\frac{1}{2}$��ACD����COF=$\frac{1}{2}$��COB��
�����ɣ���ƽ���ߵĶ��壩
�ߵ�C������OA�ϣ�
���ACD+��OCD=180�㣮
�ߡ�COB+��OCD=180�㣬
���ACD=��COB��
�����ɣ�ͬ�ǵIJ�����ȣ�
���ACE=��COF��
�ʴ�Ϊ��$\frac{1}{2}$��ACD����ƽ���ߵĶ��壬COB��ͬ�ǵIJ�����ȣ�
���� ���⿼���˽ǵļ��㣬��ƽ���ߵĶ��壬�������ս�ƽ���ߵĶ����ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪����ABC�У�AD��BE�ཻ��F����AE=EC��BD��DC=1��2����BF��FE��
��ͼ����֪����ABC�У�AD��BE�ཻ��F����AE=EC��BD��DC=1��2����BF��FE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ����3�� | C�� | ��С3�� | D�� | ��С6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6cm2 | B�� | 10cm2 | C�� | 24cm2 | D�� | 40cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 16 25 | B�� | 2 5 6 | C�� | 3 3 5 | D�� | 9 12 15 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com