
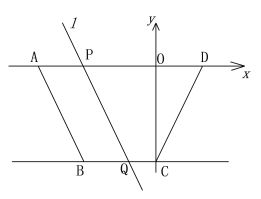
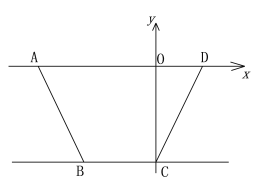
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮABCDжаЃЌADЁЮBCЃЌBC=3ЃЌБпADдкxжсЩЯЃЌЕуCдкyжсЩЯЃЌЕуDзјБъЮЊЃЈ2ЃЌ0ЃЉЃЌжБЯпlЃКy=-2x-10ОЙ§ЕуAЁЂB.
ЃЈ1ЃЉЧѓЫФБпаЮABCDЕФУцЛ§ЃЛ
ЃЈ2ЃЉНЋжБЯпlЯђгвЦНвЦЃЌЦНвЦКѓЕФжБЯпгыxжсНЛгкЕуPЃЌгыжБЯпBCНЛгкЕуQЃЌЩшAP=t.жБЯпlдкЦНвЦЙ§ГЬжаЃЌЪЧЗёДцдкtЕФжЕЃЌЪЙЁїPDQЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіtЕФжЕЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉНЋжБЯпlШЦЕуAа§зЊЃЌЕБжБЯпlНЋЫФБпаЮABCDЕФУцЛ§ЗжЮЊ1:3СНВПЗжЪБЃЌЧыжБНгаДГіlгыBCЕФНЛЕуMЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉ20ЃЛЃЈ2ЃЉДцдкЃЌt=2ЁЂ3Лђ7ЁР2![]() ЃЛЃЈ3ЃЉM1(-
ЃЛЃЈ3ЃЉM1(-![]() ЃЌ-4)ЃЌM2(
ЃЌ-4)ЃЌM2(![]() ЃЌ-4) ЃЎ
ЃЌ-4) ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнКЏЪ§НтЮіЪНЕУЕНOA=5ЃЌЧѓЕУAD=7ЃЌЕУЕНOC=4ЃЌгкЪЧЕУЕННсТлЃЛЃЈ2ЃЉашвЊЗжРрЬжТлЃЌвЊЪЙЁїPDQЮЊЕШбќШ§НЧаЮЃЌашЗжШ§жжЧщПіНјааМЦЫубщжЄЃЛЃЈ3ЃЉжБЯпlНЋЫФБпаЮABCDЕФУцЛ§ЗжЮЊ1:3СНВПЗжЪБЃЌвВЪЧашвЊЗжРрЬжТлЃЌМДжБЯпlзѓВрВПЗжУцЛ§ЃКгвВрВПЗжУцЛ§=1:3КЭЯпlгвВрВПЗжУцЛ§ЃКзѓВрВПЗжУцЛ§=1:3ЃЌдйНсКЯЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЃЌШ§НЧаЮУцЛ§МЦЫуМДПЩНтД№.
НтЃКЃЈ1ЃЉдкy=-2x-10жаЃЌЕБy=0ЪБЃЌx=-5ЃЌ
ЁрAЃЈ-5ЃЌ0ЃЉЃЌ
ЁрOA=5ЃЌ
ЁрAD=7ЃЌ
Абx=-3ДњШыy=-2x-10ЕУЃЌy=-4ЃЌ
ЁрOC=4ЃЌ
ЁрЫФБпаЮABCDЕФУцЛ§=![]() ЃЈ3+7ЃЉЁС4=20ЃЛ
ЃЈ3+7ЃЉЁС4=20ЃЛ
ЙЪД№АИЮЊЃК20ЃЛ
ЃЈ2ЃЉДцдкЃЌРэгЩШчЯТЃК
ЁпЫФБпаЮABQPЪЧЦНааЫФБпаЮЃЌЁрPQ2=AB2=42+22=20ЃЌPD2=(7-t)2ЃЌDQ2=42+(5-t)2ЃЌ
ЂйЕБPQ2= PD2ЪБЃЌМД20=(7-t)2ЃЌ
НтЕУЃКt1=7+2![]() , t2=7-2
, t2=7-2![]() ;
;
ЂкЕБPQ2= DQ2ЪБЃЌМД20=42+(5-t)2ЃЌ
НтЕУЃКt1=7ЃЈЁпAD=7ЃЌЁрt1=7ЪБЃЌP,DЕужиКЯЃЌВЛЗћКЯЬтвтЃЌЩсШЅЃЉ , t2=3;
ЂлЕБPD2= DQ2ЪБЃЌМД(7-t)2=42+(5-t)2ЃЌ
НтЕУЃКt=2ЃЌ
злЩЯЫљЪіЃКЕБt=2ЃЌ3Лђ7ЁР2![]() ЪБЃЌЁїPDQЮЊЕШбќШ§НЧаЮЃЛ
ЪБЃЌЁїPDQЮЊЕШбќШ§НЧаЮЃЛ
ЃЈ3ЃЉЂйШчЭМЃКЕБЕуMдкЯпЖЮBCЩЯЪБЃЌМДжБЯпlзѓВрВПЗжУцЛ§ЃКгвВрВПЗжУцЛ§=1:3ЃЌ
ЁрSЁїABM=![]() SЫФБпаЮABCD=5 ЃЌЁпOC=4ЃЌЁрBMЩЯЕФИпhBM=4,
SЫФБпаЮABCD=5 ЃЌЁпOC=4ЃЌЁрBMЩЯЕФИпhBM=4,
ЁрSЁїABM=![]() ЁСBMЁСhBM=5ЃЌМД
ЁСBMЁСhBM=5ЃЌМД![]() ЁСBMЁС4=5ЃЌНтЕУBM=
ЁСBMЁС4=5ЃЌНтЕУBM=![]() ЃЌ
ЃЌ
ЁрCM=BC-BM=3-![]() =
=![]() ,
,
гжЁпBCЁЮxжсЃЌC(0ЃЌ-4)ЃЌMЕудкЕкШ§ЯѓЯоЃЌ
ЁрMЕуЕФзјБъЮЊM1(-![]() ЃЌ-4)ЃЛ
ЃЌ-4)ЃЛ
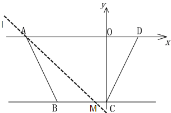
ЂкШчЭМЃКЁпAD=7ЃЌOC=4ЃЌЁрЁїACDЕФУцЛ§=7ЁС4ЁТ2=14>5,
ЁрЕБжБЯпlгвВрВПЗжУцЛ§ЃКзѓВрВПЗжУцЛ§=1:3ЪБЃЌЕуMОЭдкЕуCЕФгвВрЃЌЩшДЫЪБAMгыCDЕФНЛЕуЮЊЕуNЃЌЁїANDжаADБпЕФИпЮЊhADЃЌЁїCNMжаCMБпЕФИпЮЊhCMЃЌ
ДЫЪБЃКSЁїAND=![]() ЁСADЁСhAD=5ЃЌМД
ЁСADЁСhAD=5ЃЌМД![]() ЁС7ЁСhAD=5ЃЌНтЕУЃКhAD=
ЁС7ЁСhAD=5ЃЌНтЕУЃКhAD=![]() ЃЌ
ЃЌ
ЁпADЁЮCMЃЌAD=7ЃЌOC=4ЃЌ CMЩЯЕФИпhCM =4- ![]() =
=![]() ЃЌ ЁрЁїANDЁзЁїMNCЃЌ
ЃЌ ЁрЁїANDЁзЁїMNCЃЌ
ЁрAD:CM= hAD: hCM,МДЃК7ЃКCM=![]() :
:![]() ЃЌНтЕУЃКCM=
ЃЌНтЕУЃКCM=![]() ,
,
ЁрMЕуЕФзјБъЮЊM1(![]() ЃЌ-4)ЃЛ
ЃЌ-4)ЃЛ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
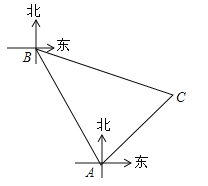
ЁОЬтФПЁПЃЈ6ЗжЃЉФГКЃгђгаAЃЌBСНИіИлПкЃЌBИлПкдкAИлПкББЦЋЮї30ЁуЗНЯђЩЯЃЌОрAИлПк60КЃРяЃЌгавЛЫвДЌДгAИлПкГіЗЂЃЌбиЖЋББЗНЯђааЪЛвЛЖЮОрРыКѓЃЌЕНДяЮЛгкBИлПкФЯЦЋЖЋ75ЁуЗНЯђЕФCДІЃЌЧѓИУДЌгыBИлПкжЎМфЕФОрРыМДCBЕФГЄЃЈНсЙћБЃСєИљКХЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНЉx2+bx+cгывЛжБЯпЯрНЛгкAЃЈ1ЃЌ0ЃЉЁЂCЃЈЉ2ЃЌ3ЃЉСНЕуЃЌгыyжсНЛгкЕуNЃЌЦфЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпМАжБЯпACЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШєPЪЧХзЮяЯпЩЯЮЛгкжБЯпACЩЯЗНЕФвЛИіЖЏЕуЃЌЧѓЁїAPCЕФУцЛ§ЕФзюДѓжЕМАДЫЪБЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЖдГЦжсЩЯЪЧЗёДцдквЛЕуMЃЌЪЙЁїANMЕФжмГЄзюаЁЃЎШєДцдкЃЌЧыЧѓГіMЕуЕФзјБъКЭЁїANMжмГЄЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
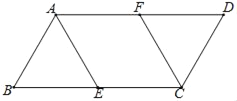
ЁОЬтФПЁПШчЭМЃЌдкЦНааЫФБпаЮABCDжаЃЌ![]() ЃЌЕуEЁЂFЗжБ№ЪЧBCЁЂADЕФжаЕуЃЎ
ЃЌЕуEЁЂFЗжБ№ЪЧBCЁЂADЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() Ёе
Ёе![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓЫФБпаЮAECFЕФУцЛ§ЃЎ
ЪБЃЌЧѓЫФБпаЮAECFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїADEОљЮЊЕШбќжБНЧШ§НЧаЮЃЌСЌНгBEЃЌЕуFЁЂGЗжБ№ЮЊADЁЂACЕФжаЕуЃЌСЌНгFGЃЎдкЁїADEШЦAа§зЊЕФЙ§ГЬжаЃЌЕБBЁЂDЁЂEШ§ЕуЙВЯпЪБЃЌAB=![]() ЃЌAD=1ЃЌдђЯпЖЮFGЕФГЄЮЊ___ЃЎ
ЃЌAD=1ЃЌдђЯпЖЮFGЕФГЄЮЊ___ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩНЕиздааГЕдНРДдНЪмЕНжабЇЩњЕФЯВАЎЃЌИїжжЦЗХЦЯрМЬЭЖЗХЪаГЁЃЌФГГЕааОгЊЕФAаЭГЕШЅФъЯњЪлзмЖюЮЊ5ЭђдЊЃЌНёФъУПСОЯњЪлМлБШШЅФъНЕЕЭ400дЊЃЌШєТєГіЕФЪ§СПЯрЭЌЃЌЯњЪлзмЖюНЋБШШЅФъМѕЩй20%ЃЎ
ЃЈ1ЃЉНёФъAаЭГЕУПСОЪлМлЖрЩйдЊЃПЃЈгУСаЗНГЬЕФЗНЗЈНтД№ЃЉ
ЃЈ2ЃЉИУГЕааМЦЛЎаТНјвЛХњAаЭГЕКЭаТПюBаЭГЕЙВ60СОЃЌЧвBаЭГЕЕФНјЛѕЪ§СПВЛГЌЙ§AаЭГЕЪ§СПЕФСНБЖЃЌгІШчКЮНјЛѕВХФмЪЙетХњГЕЛёРћзюЖрЃП
AЃЌBСНжжаЭКХГЕЕФНјЛѕКЭЯњЪлМлИёШчЯТБэЃК
AаЭГЕ | BаЭГЕ | |
НјЛѕМлИёЃЈдЊЃЉ | 1100 | 1400 |
ЯњЪлМлИёЃЈдЊЃЉ | НёФъЕФЯњЪлМлИё | 2000 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌABЮЊАыдВOЕФжБОЖЃЌDЮЊBAЕФбгГЄЯпЩЯвЛЕуЃЌDCЮЊАыдВOЕФЧаЯпЃЌЧаЕуЮЊCЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯACD=ЁЯBЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЁЯBDCЕФЦНЗжЯпЗжБ№НЛACЃЌBCгкЕуEЃЌFЃЛ
ЂйЧѓtanЁЯCFEЕФжЕЃЛ
ЂкШєAC=3ЃЌBC=4ЃЌЧѓCEЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
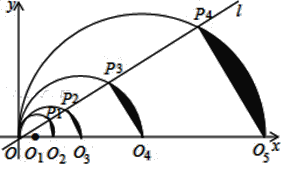
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпlЕФКЏЪ§БэДяЪНЮЊy=![]() xЃЌЕуO1ЕФзјБъЮЊ(1ЃЌ0)ЃЌвдO1ЮЊдВаФЃЌO1OЮЊАыОЖЛАыдВЃЌНЛжБЯпlгкЕуP1ЃЌНЛxжсе§АыжсгкЕуO2ЃЌгЩЯвP1O2КЭ
xЃЌЕуO1ЕФзјБъЮЊ(1ЃЌ0)ЃЌвдO1ЮЊдВаФЃЌO1OЮЊАыОЖЛАыдВЃЌНЛжБЯпlгкЕуP1ЃЌНЛxжсе§АыжсгкЕуO2ЃЌгЩЯвP1O2КЭ![]() ЮЇГЩЕФЙаЮУцЛ§МЧЮЊS1ЃЌвдO2ЮЊдВаФЃЌO2OЮЊАыОЖЛдВЃЌНЛжБЯпlгкЕуP2ЃЌНЛxжсе§АыжсгкЕуO3ЃЌгЩЯвP2O3КЭЮЇ
ЮЇГЩЕФЙаЮУцЛ§МЧЮЊS1ЃЌвдO2ЮЊдВаФЃЌO2OЮЊАыОЖЛдВЃЌНЛжБЯпlгкЕуP2ЃЌНЛxжсе§АыжсгкЕуO3ЃЌгЩЯвP2O3КЭЮЇ![]() ГЩЕФЙаЮУцЛ§МЧЮЊS2ЃЌвдO3ЮЊдВаФЃЌO3OЮЊАыОЖЛдВЃЌНЛжБЯпlгкЕуP3ЃЌНЛxжсе§АыжсгкЕуO4ЃЌгЩЯвP3O4КЭ
ГЩЕФЙаЮУцЛ§МЧЮЊS2ЃЌвдO3ЮЊдВаФЃЌO3OЮЊАыОЖЛдВЃЌНЛжБЯпlгкЕуP3ЃЌНЛxжсе§АыжсгкЕуO4ЃЌгЩЯвP3O4КЭ![]() ЮЇГЩЕФЙаЮУцЛ§МЧЮЊS3ЃЛЁАДДЫзіЗЈНјааЯТШЅЃЌЦфжаS2018ЕФУцЛ§ЮЊ__________ЃЎ
ЮЇГЩЕФЙаЮУцЛ§МЧЮЊS3ЃЛЁАДДЫзіЗЈНјааЯТШЅЃЌЦфжаS2018ЕФУцЛ§ЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
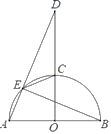
ЁОЬтФПЁПШчЭМЃЌвбжЊABЪЧАыдВOЕФжБОЖЃЌOCЁЭABНЛАыдВгкЕуCЃЌDЪЧЩфЯпOCЩЯвЛЕуЃЌСЌНсADНЛАыдВOгкЕуEЃЌСЌНсBEЃЌCEЃЎ
ЃЈ1ЃЉЧѓжЄЃКECЦНЗжЁЯBEDЃЎ
ЃЈ2ЃЉЕБEBЃНEDЪБЃЌЧѓжЄЃКAEЃНCEЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com