
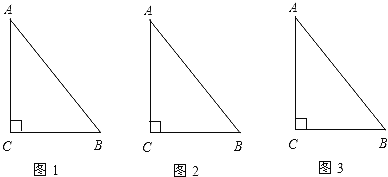
【题目】有一块直角三角形的绿地,量得两直角边长分别为6m和8m,现在要将绿地扩充成等腰三角形,且扩充部分是以8m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
【答案】扩充后的绿地周长为32m或(20+4![]() )m或
)m或![]() m.
m.
【解析】
根据题意画出图形,构造出等腰三角形,根据等腰三角形及直角三角形的性质利用勾股定理解答.
在Rt△ABC中,∠ACB=90°,AC=8,BC=6
由勾股定理有:AB=10,应分以下三种情况:
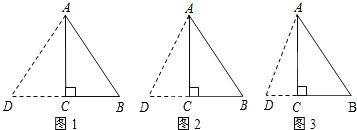
①如图1,当AB=AD=10时,
∵AC⊥BD,
∴CD=CB=6m,
∴△ABD的周长=10+10+2×6=32m;
②如图2,当AB=BD=10时,
∵BC=6m,
∴CD=10-6=4m,
∴AD=![]() =4
=4![]() m,
m,
∴△ABD的周长=10+10+4![]() =(20+4
=(20+4![]() )m;
)m;
③如图3,当AB为底时,设AD=BD=x,则CD=x-6,
由勾股定理得:AD2=AC2+CD2,
即82+(x-6)2=x2,
解得,x=![]() ,
,
∴△ABD的周长为:AD+BD+AB=![]() +
+![]() +10=
+10=![]() m,
m,
综上可知,扩充后的绿地周长为32m或(20+4![]() )m或
)m或![]() m.
m.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明、小亮从保安中心图书馆出发,沿相同的线路跑向保安体育场,小明先跑一点路程后,小亮开始出发,当小亮超过小明150米时,小亮停在此地等候小明,两人相遇后,一起以小明原来的速度跑向宝安体育场,如图,反映了两人所跑路程y(米)与所用时间x(秒)之间的关系,请根据题意解答下列问题:
(1)问题中的自变量是________,因变量是_________;
(2) 小明共跑了________米,小明的速度为________米/秒;
(3) 图中a=________米,小亮在途中等候小明的时间是________秒;
(4)小亮从A跑到B这段的速度为________米/秒;
(5)求出b的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C.

(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴ (同角的补角相等)①
∴ (内错角相等,两直线平行)②
∴∠ADE=∠3( )③
∵∠3=∠B( )④
∴ (等量代换)⑤
∴DE∥BC( )⑥
∴∠AED=∠C( )⑦

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区对参加2019年中考的300名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图.

请根据图表信息回答下列问题:
(1)![]() __________,
__________,![]() __________;
__________;
(2)将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均为正常,据以上信息估计全区初中毕业生中视力正常的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC, FD=CD。求证:(1) Rt△BDF≌Rt△ADC (2) BE⊥AC
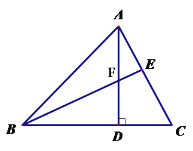
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个转盘被分成6个相等的扇形,颜色分为红、绿、黄三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,重新转动).下列事件:①指针指向红色;②指针指向绿色;(③指针指向黄色;④指针不指向黄色,估计各事件的可能性大小,完成下列问题.
(1)④事件发生的可能性大小是 ;
(2)多次实验,指针指向绿色的频率的估计值是 ;
(3)将这些事件的序号按发生的可能性从小到大的顺序排列为: ![]()
![]()
![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com