
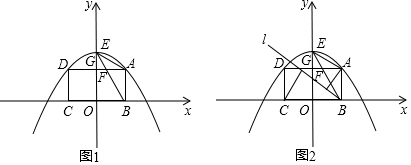
���� ��1��������y���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ���ݾ��ε��ܳ��г����̼��ɽ�����⣻
��2����ͼ1�У����ȹ������κ���֤��DE��BE����֤��A��B��D��E�ĵ㹲Բ�����ɽ�����⣻
��3���ٹ۲�ͼ�ο�֪����AEB�ǵ���������ʱ��ֻ��AE=AB����Rt��AEG�У�����AE2=EG2+AG2���ɵã�-a2+1��2=��1+a2-1��2+a2�����a���ɽ�����⣮
����ͼ3�У�����A��AM��ֱ��l��CP��ֱ��l��P��AH��ֱ��L��H���ӳ�CP��AM��M�����ı���AHPM�Ǿ��Σ���PM=AH=d1���Ƴ�d1+d2=CP+AH=CP+PM=CM��
��������d1+d2�����ֵ��ֻҪ��CM�����ֵ���ɣ�����M���A�غ�ʱCM��ֵ���
��� �⣺��1��������y���������ߵĶԳ��ᣬҲ�Ǿ���ABCD�ĶԳ��ᣬ
��A��D����y��Գƣ�
��DG=AG��
��A��a��-a2+1����
������2[2a+��-a2+1��]=3.5��
���a=$\frac{1}{2}$��$\frac{3}{2}$����������
��a=$\frac{1}{2}$��
��2����ͼ1�У�
��A��a��-a2+1����E��0��1����D��-a��-a2+1����
��ֱ��EB�Ľ���ʽΪy=-$\frac{1}{a}$x+1��ֱ��DE�Ľ���ʽΪy=ax+1��
��-$\frac{1}{a}$��a=-1��
��DE��EB����BD��OE��P��
��PG��AB��DG=GA��
��DP=PB��
��PD=PE=PA=PB��
��A��B��D��E�ĵ㹲Բ��
��$\widehat{DE}$=$\widehat{DE}$��
���EAD=��ABE��
��3��?�۲�ͼ�ο�֪����AEB�ǵ���������ʱ��ֻ��AE=AB��
��Rt��AEG����AE2=EG2+AG2��
�ࣨ-a2+1��2=��1+a2-1��2+a2��
���a=$\frac{\sqrt{3}}{3}$��-$\frac{\sqrt{3}}{3}$����������
���A��$\frac{\sqrt{3}}{3}$��$\frac{2}{3}$����
����ͼ3�У�����A��AM��ֱ��l��CP��ֱ��l��P��AH��ֱ��L��H���ӳ�CP��AM��M�����ı���AHPM�Ǿ��Σ�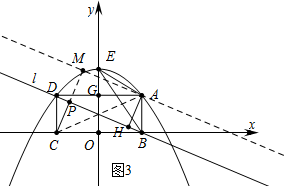
��PM=AH=d1��
��d1+d2=CP+AH=CP+PM=CM��
����d1+d2�����ֵ��ֻҪ��CM�����ֵ���ɣ�
��Rt��ACM��CM��AC��
�൱��M���A�غ�ʱCM��ֵ���ʱCM=CA��
��d1+d2�����ֵ=AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{��\frac{2\sqrt{3}}{3}��^{2}+��\frac{2}{3}��^{2}}$=$\frac{4}{3}$��
���� ���⿼����κ����ۺ��⡢һ�κ��������ʡ����ε����ʡ�Բ���й�֪ʶ�����ɶ�����֪ʶ������Ĺؼ���ѧ�����Ӹ���Բ������Բ���й�֪ʶ������⣬ѧ����ת����˼��˼�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���ABC�͡�ACB�����ƽ���߽���D����A=50�㣬��ô��D=65�㣮
��ͼ���ڡ�ABC�У���ABC�͡�ACB�����ƽ���߽���D����A=50�㣬��ô��D=65�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABCD�����Σ��Խ���AC=8cm��BD=6cm��DH��AB�ڵ�H����AB=5��DH=$\frac{24}{5}$��
��ͼ���ı���ABCD�����Σ��Խ���AC=8cm��BD=6cm��DH��AB�ڵ�H����AB=5��DH=$\frac{24}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
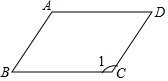 ���ı���ABCD�У���֪��B=60�㣬��1=120�㣬AB��CDƽ����AD��BCƽ����
���ı���ABCD�У���֪��B=60�㣬��1=120�㣬AB��CDƽ����AD��BCƽ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
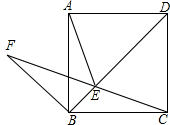 ��ͼ��ʾ����������ABCD�ĶԽ���BD��ȡһ��E��ʹ�á�BAE=15�㣬����AE��CE���ӳ�CE��F������BF��ʹ��BC=BF����AB=1�������н��ۣ���AE=EC����F��BC�ľ���Ϊ$\frac{\sqrt{2}}{2}$����BE+EC=EF����S��EBF=$\frac{\sqrt{3}}{12}$��������ȷ���۵�����Ǣ٢ۢܣ�
��ͼ��ʾ����������ABCD�ĶԽ���BD��ȡһ��E��ʹ�á�BAE=15�㣬����AE��CE���ӳ�CE��F������BF��ʹ��BC=BF����AB=1�������н��ۣ���AE=EC����F��BC�ľ���Ϊ$\frac{\sqrt{2}}{2}$����BE+EC=EF����S��EBF=$\frac{\sqrt{3}}{12}$��������ȷ���۵�����Ǣ٢ۢܣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com