
【题目】已知凸四边形ABCD中,∠A=∠C=90°.
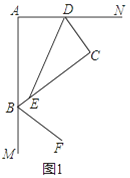
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明.
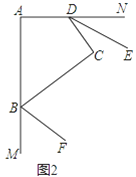
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明.
【答案】见解析
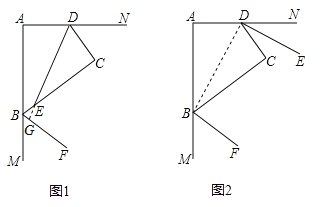
【解析】试题分析:(1)DE⊥BF,延长DE交BF于G.易证∠ADC=∠CBM.可得∠CDE=∠EBF.即可得∠EGB=∠C=90゜,则可证得DE⊥BF;
(2)DE∥BF,连接BD,易证∠NDC+∠MBC=180゜,则可得∠EDC+∠CBF=90゜,继而可证得∠EDC+∠CDB+∠CBD+∠FBC=180゜,则可得DE∥BF.
试题解析:解:(1)DE⊥BF.证明如下:
延长DE交BF于点G.∵∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,∴∠ABC+∠ADC=180°.∵∠ABC+∠MBC=180°,∴∠ADC=∠MBC.∵DE、BF分别平分∠ADC、∠MBC,∴∠EDC=![]() ∠ADC,∠EBG=
∠ADC,∠EBG=![]() ∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
∠MBC,∴∠EDC=∠EBG.∵∠EDC+∠DEC+∠C=180°,∠EBG+∠BEG+∠EGB=180°,∠DEC=∠BEG,∴∠EGB=∠C=90°,∴DE⊥BF;
(2)DE∥BF.证明如下:
连接BD.∵DE、BF分别平分∠NDC、∠MBC,∴∠EDC=![]() ∠NDC,∠FBC=
∠NDC,∠FBC=![]() ∠MBC.
∠MBC.
∵∠ADC+∠NDC=180°,∠ADC=∠MBC,∴∠MBC+∠NDC=180°,∴∠EDC+∠FBC=90°.
∵∠C=90°,∴∠CDB+∠CBD=90°,∴∠EDC+∠CDB+∠FBC+∠CBD=180°,即∠EDB+∠FBD=180°,∴DE∥BF.


科目:初中数学 来源: 题型:
【题目】骰子是一种特别的数字立方体(见下图),它符合规则:相对两面的点数之和总是7,下面四幅图中可以折成符合规则的骰子的是( )
![]()
A.  B.
B.  C.
C. 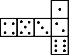 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径AB=4,以长为2的弦PQ为直径,向点O方向作半圆M,其中P点在 ![]() 上且不与A点重合,但Q点可与B点重合.
上且不与A点重合,但Q点可与B点重合. 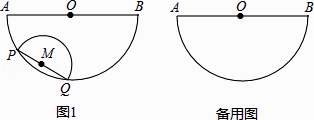
发现: ![]() 的长与
的长与 ![]() 的长之和为定值l,求l:
的长之和为定值l,求l:
查看答案和解析>>
科目:初中数学 来源: 题型:
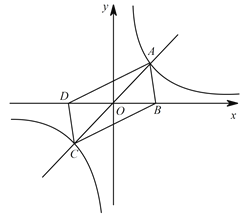
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于
的图象分别交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 与点
与点![]() 关于坐标原点
关于坐标原点![]() 成中心对称,且点
成中心对称,且点![]() 的坐标为
的坐标为![]() .其中
.其中![]() .
.
(1)四边形![]() 是 .(填写四边形
是 .(填写四边形![]() 的形状)
的形状)
(2)当点![]() 的坐标为
的坐标为![]() 时,且四边形
时,且四边形![]() 是矩形,求
是矩形,求![]() ,
,![]() 的值.
的值.
(3)试探究:随着![]() 与
与![]() 的变化,四边形
的变化,四边形![]() 能不能成为菱形?若能,请直接写出
能不能成为菱形?若能,请直接写出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现
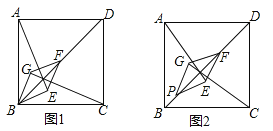
(1)正方形ABCD中有菱形PEFG,当它们的对角线重合,且点P与点B重合时(如图1),通过观察或测量,猜想线段AE与CG的数量关系,并证明你的猜想;
(2)当(1)中的菱形PEFG沿着正方形ABCD的对角线平移到如图2的位置时,猜想线段AE与CG的数量关系,只写出猜想不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
(1)如果点P到点A,点B的距离相等,那么x=______;
(2)若点P到点A,点B的距离之和最小,则整数x是____________ ;
(3)当点P到点A,点B的距离之和是6时,求x的值;
(4)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动、点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动多少秒时,点P到点E,点F的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:当黑色瓷砖为28块时,白色瓷砖块数为( )
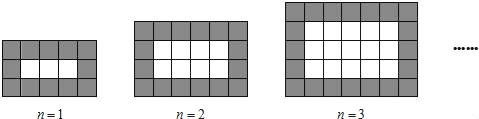
A. 27 B. 28 C. 33 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com