
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
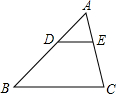 如图,△ABC中,DE∥BC,若$\frac{AD}{BD}$=$\frac{2}{3}$,若△ADE的面积为4,则四边形DBCE的面积为( )
如图,△ABC中,DE∥BC,若$\frac{AD}{BD}$=$\frac{2}{3}$,若△ADE的面积为4,则四边形DBCE的面积为( )| A. | 3 | B. | 9 | C. | 5 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 要给一个长、宽、高分别为x,y,z的箱子打包,其打包方式如图所示.
要给一个长、宽、高分别为x,y,z的箱子打包,其打包方式如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
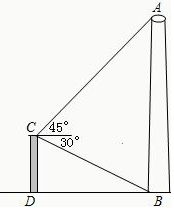 如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在城市改造时,要拆除建筑物AB,在离它21米远的建筑物CD顶端C测得A的仰角45°,B的俯角30°,在点B的35米处有一文物,问:此文物是否在危险区内?请说明理由.(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
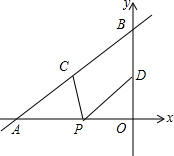 如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )
如图,直线y=$\frac{2}{3}$x+4与x轴,y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,则PC+PD的最小值为( )| A. | 2+$\sqrt{13}$ | B. | 5 | C. | 2$\sqrt{13}$ | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com