
 如图,⊙O的半径为3,过点A(5,0)的直线与⊙O相切于点B,与y轴正半轴相交于点C.
如图,⊙O的半径为3,过点A(5,0)的直线与⊙O相切于点B,与y轴正半轴相交于点C.分析 (1)运用切线的性质,借助勾股定理即可求出AB的长度;
(2)首先运用射影定理求出BC的长度,进而运用勾股定理求出OC的长度,借助待定系数法即可解决问题.
解答 解:(1)如图,连接OB;
∵直线AB与⊙O相切于点B,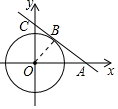
∴OB⊥AB;
由勾股定理得:
AB2=AO2-OB2=25-9=16,
∴AB=4;
(2)∵OB是直角△AOC的斜边AC上的高,
∴OB2=AB•BC(射影定理),
∴BC=$\frac{9}{4}$;
由勾股定理得:
OC=$\sqrt{O{B}^{2}+B{C}^{2}}$=$\frac{15}{4}$,
∴点C的坐标为(0,$\frac{15}{4}$),
将A、C两点的坐标代入y=kx+b得:
$\left\{\begin{array}{l}{0=5k+b}\\{\frac{15}{4}=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{15}{4}}\end{array}\right.$.
点评 该命题以平面直角坐标系为载体,以圆的切线的性质、待定系数法为考查的核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
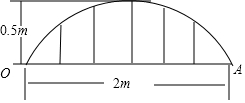 某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com