
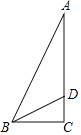
【题目】如图,△ABC中,∠C=90°,点D为AC上一点,∠ABD=2∠BAC=45°,若AD=12,则△ABD的面积为____.
【答案】36.
【解析】
作DE⊥DB交AB于E,EF垂直AC于F,则∠DEB=90°-∠ABD=45°,证出AE=DE=DB,通过证明△AEF≌△BCD,得出BC==AF=![]() AD=6,由三角形面积公式即可得出答案.
AD=6,由三角形面积公式即可得出答案.
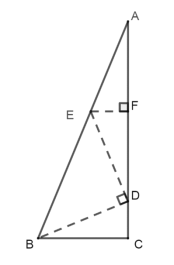
作DE⊥DB交AB于E,EF垂直AC于F,如图所示:
则∠DEB=90°-∠ABD=45°,
∴△BDE是等腰直角三角形,
∴DB=DE,
∵∠ABD=2∠BAC=45°,
∴∠BAC=22.5°,
∴∠ADE=∠DEB-∠BAC=22.5°=∠BAC,
∴AE=DE=DB,
∵∠AFE=90°,
∴F是AD中点,AF=FD,
又∵∠C=90°,
∴∠CBD=90°-45°-22.5°=22.5°,
在Rt△AEF和Rt△BCD中

∴Rt△AEF≌Rt△BCD(AAS),
∴AF=BC=![]() AD=6,
AD=6,
∴△ABD的面积S=![]() AD×BC=
AD×BC=![]() ×12×6=36;
×12×6=36;
故答案为:36.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A,B两种品牌的龟苓膏粉共1000包.
(1)若小王按需购买A,B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式;
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本?(运算结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
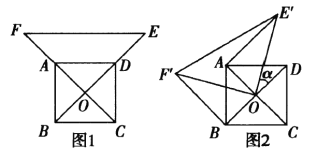
【题目】如图1,O为正方形![]() 的中心,分别延长OA、OD到点
的中心,分别延长OA、OD到点![]() ,使OF=2OA,OE
,使OF=2OA,OE![]() ,连接EF,将
,连接EF,将![]() 绕点O按逆时针方向旋转角
绕点O按逆时针方向旋转角![]() 得到
得到![]() ,连接
,连接![]() (如图2).
(如图2).
(1)探究![]() 与
与![]() 的数量关系,并给予证明;
的数量关系,并给予证明;
(2)当![]() 时,求证:
时,求证:![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张三角形纸片沿DE折叠,当点A落在四边形BCED的内部时,∠A、∠1、∠2之间的关系是( )
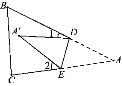
A. ∠A=∠1+∠2 B. 2∠A=∠1+∠2
C. 3∠A=∠1+∠2 D. 4∠A=∠1+∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
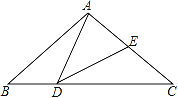
【题目】如图,△ABC中,AB=AC=2,∠B=∠C=40°.点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BAD=20°时,∠EDC= °;
(2)当DC等于多少时,△ABD≌△DCE?试说明理由;
(3)△ADE能成为等腰三角形吗?若能,请直接写出此时∠BAD的度数;若不能,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
(1)求一次函数与反比例函数的解析式;
(2)记两函数图象的另一个交点为E,求△CDE的面积;
(3)直接写出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
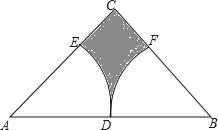
【题目】如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AB=4,则图中阴影部分的面积为_____(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知直线
,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,以
,以![]() 为边在第一象限内作长方形
为边在第一象限内作长方形![]() .
.
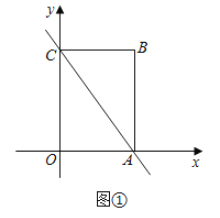
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 .
的坐标为 .
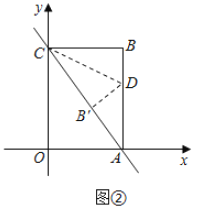
(2)如图![]() ,将△ABC对折,使得点
,将△ABC对折,使得点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 交
交![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在第一象限内,是否存在点![]() (点
(点![]() 除外),使得
除外),使得![]() 与
与![]() 全等?若存在,请求出点
全等?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com