
����Ŀ�������仯�����Ѿ�����������ĸ߶ȹ�ע���йز�����ȫ����Χ�ڶ�12��35��������Ⱥ�����˼�����������飬���Ƴ���������ͳ��ͼ��

�����ͼ�е���Ϣ���ش��������⣺
��1����γ��������й������������ˣ�
��2���벹ȫ����ͳ��ͼ��
��3������ͳ��ͼ��18��23�겿�ֵ�Բ�ĽǵĶ�����������
��4���ݱ�����Ŀǰ�ҹ�12��35���������ԼΪ2000�����������12��23�������
���𰸡�(1)a=300��(2)108����(3)12��23�������Ϊ400��
�������������������1������30-35�����������ռ�İٷֱ�������������
��2���ӵ�����������м�ȥ��֪����������������ɵõ�12-17����������ݴ˲�ȫ����ͳ��ͼ��
��3���ȼ���18-23�������ռ�����������İٷֱȣ��ټ�����һ������Ӧ��Բ�ĽǵĶ�����
��4���ȼ��������12��23���������ռ�İٷֱȣ������������ԼΪ2000���е�12��23���������
����������⣺��1���������ͳ��ͼ������ͳ��ͼ��֪��30-35�������Ϊ330�ˣ���ռ�İٷֱ�Ϊ22%�����Ե����������Ϊ330��22%=1500�ˣ�
�ʴ�Ϊ��1500 ��
��2��1500-450-420-330=300�ˣ�
��ȫ������ͳ��ͼ��ͼ��

��3��18-23����һ������Ӧ��Բ�ĽǵĶ���Ϊ360��![]() =108����
=108����
�ʴ�Ϊ��108�� ��
��4����300+450����1500=50%��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C=90�㣬AC=BC��ADƽ�֡�CAB��BC��D��DE��AB��E��AB=6cm�����DEB���ܳ�Ϊ�� �� 
A.40cm
B.6cm
C.8cm
D.10cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�鳤Ϊa�ס���Ϊb�ij����οյأ��ּƻ������յ��м����������ഹֱ�Ŀ���Ϊ2�ĵ�·��ͼ����Ӱ���֣������ಿ�ֽ����̻��� 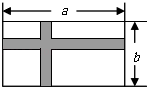
��1������̵ص���������ú�a��b�Ĵ���ʽ��ʾ��
��2����a=2b���ҵ�·�����Ϊ116��2 �� ��ԭ�����οյصĿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O���߶�AB�ϣ���C��D�ֱ���AO��BO���е㣮
(1)AO��________CO��BO��________DO��
(2)��CO��3cm��DO��2cm�����߶�AB�ij��ȣ�
(3)���߶�AB��10��С�������ɵ����CD��5.���ڷ�˼������ͻ�����룺����O���߶�AB���ӳ����ϣ�ԭ�еĽ��ۡ�CD��5���Ƿ���Ȼ�����أ����С������ͼ�η�������˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��2��1������ƽ��2����λ��õ�P������P���������ǣ� ��
A.��2��3��
B.��2��-1��
C.��4��1��
D.��0��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������κ���y=2��x��3��2��4ͼ��ĶԳ���Ϊֱ��l������M��ֱ��l�ϣ����M����������ǣ� ��
A.��1��0��
B.��3��0��
C.��0����4��
D.����3��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ��ѧ����һ��������Ϸ������ѧ���������²�����м��㣺
������һ����λ��a����a����2���ټ���9�������õĺ��ٳ���2��
�ڰ�a����2���ټ���30�������õĺͳ���2��
�۰Ѣ����õĽ����ȥ�����õĽ��������Ϊ���Ľ����
����ʦ˵��ֻҪ����������Ľ�����Ҿ��ܲ³�����������λ��a��
ѧ������������Ľ����96������ʦ�����³���������������λ����31��
�����
��1���ɢٿ��д���ʽ�� �����ɢڿ��д���ʽ�� �����ɢۿ�֪�����Ϊ�� �������ú�a��ʽ�ӱ�ʾ��
��2��ѧ��С������Ľ����120�����ܲ³�����������λ���Ƕ�����
��3�������Լ������Խ��ͳ���ʦ�����ķ�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com