
【题目】如图,分别以![]() 的直角边
的直角边![]() 和斜边
和斜边![]() 为边向外作正方形
为边向外作正方形![]() 和正方形
和正方形![]() ,连结
,连结![]() 、
、![]() 、
、![]() .给出下列结论:
.给出下列结论:
①![]() ;
;
②![]()
③![]()
④![]() 其中正确的是( )
其中正确的是( )
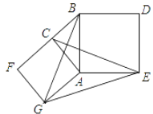
A.②③④B.①②③C.①②④D.①②③④
【答案】C
【解析】
利用SAS证明△AGB≌△ACE,即可判断①;证明∠BNM=∠MAE=90![]() ,即可判断②;假设③成立,利用勾股定理对等式变形证得
,即可判断②;假设③成立,利用勾股定理对等式变形证得![]() =
=![]() ,而
,而![]() 与
与![]() 不一定相等,即可判断③;利用勾股定理证得
不一定相等,即可判断③;利用勾股定理证得![]() ,从而证得结论④成立.
,从而证得结论④成立.
∵四边形![]() 和四边形
和四边形![]() 都是正方形,
都是正方形,
∴AC=AG,AB=AE,
∵∠CAG=∠BAE=90°,
∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,
在△AGB和△ACE中,
∵ ,
,
∴△AGB≌△ACE(SAS),
∴GB=CE,故①正确;
设BA、CE相交于点M,
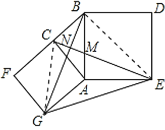
∵△AGB≌△ACE,
∴∠GBA=∠CEA,
又∵∠BMN=∠EMA,
∴∠BNM=∠MAE=90![]() ,
,
∴![]() ,故②正确;
,故②正确;
设正方形![]() 和正方形
和正方形![]() 的边长分别为
的边长分别为![]() 和
和![]() ,
,
∵![]() 为直角三角形,且
为直角三角形,且![]() 为斜边,
为斜边,
∴![]() ,
,
假设![]() 成立,
成立,
则有![]() ,
,
整理得:![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() 与
与![]() 不一定相等,
不一定相等,
∴假设不成立,故③不正确;
连接CG,BE,设BG、CE相交于N,
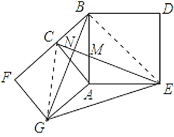
∵![]() ,
,
∴![]() ,
,
∵四边形![]() 和四边形
和四边形![]() 都是正方形,
都是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,故④正确;
,故④正确;
综上,①②④正确,


科目:初中数学 来源: 题型:
【题目】我国边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防部迅速派出快艇B追赶(如图1).图2中l1、l2分别表示两船相対于海岸的距离s(海里)与追赶时间t(分)之间的关系.根据图象问答问题:
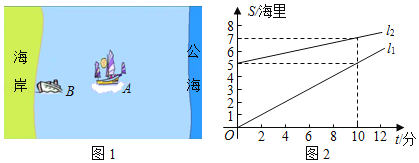
(1)①直线l1与直线l2中 表示B到海岸的距离与追赶时间之间的关系
②A与B比较, 速度快;
③如果一直追下去,那么B (填能或不能)追上A;
④可疑船只A速度是 海里/分,快艇B的速度是 海里/分
(2)l1与l2对应的两个一次函数表达式S1=k1t+b1与S2=k2t+b2中,k1、k2的实际意义各是什么?并直接写出两个具体表达式
(3)15分钟内B能否追上A?为什么?
(4)当A逃离海岸12海里的公海时,B将无法对其进行检查,照此速度,B能否在A逃入公海前将其拦截?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
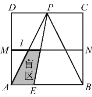
【题目】如图,正方形ABCD的边长为4,M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的左端点从M点开始,运动时间为t秒(0≤t≤3).设△PAB区域内的盲区面积为y(平方单位).
(1)求y与t之间的函数关系式;
(2)请简单概括y随t的变化而变化的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
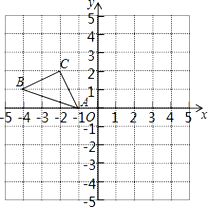
(1)试作出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;点B1的坐标为 ;
(2)作△ABC关于原点O成中心对称的△A2B2C2;点B2的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,先对折矩形得折痕MN,再折纸使折线过点B,且使得A在MN上,这时折线EB与BC所成的角为( )
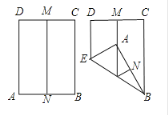
A.30°B.45°C.60°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“面线”,“面线”被这个平面图形截得的线段叫做该图形的“面径”(例如圆的直径就是它的“面径”).已知等边三角形的边长为4,则它的“面径”长x的取值范围是 _.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:(1)已知:如图①,在![]() 和
和![]() 中,OA=OB,OC=OD,
中,OA=OB,OC=OD,![]() ,求证:①AC=BD;②
,求证:①AC=BD;②![]() .
.
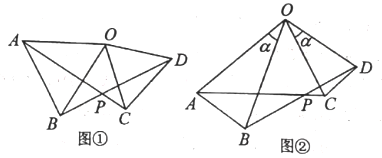
(2)如图②,在![]() 和
和![]() 中,若OA=OB,OC=OD,
中,若OA=OB,OC=OD,![]() ,则AC与BD间的等量关系式为 ;
,则AC与BD间的等量关系式为 ;![]() 的大小为 .
的大小为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
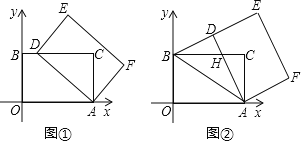
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图①,当点D落在BC边上时,求点D的坐标;
(2)如图②,当点D落在线段BE上时,AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com