练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．不等式6-4x≥3x-8的非负整数解为（　　）
    A．2个B．3个C．4个D．5个

    分析 首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的非负整数即可．

    解答 解：移项得，-4x-3x≥-8-6，
    合并同类项得，-7x≥-14，
    系数化为1得，x≤2．
    故其非负整数解为：0，1，2，共3个．
    故选B．

    点评 本题考查了一元一次不等式的整数解，正确解不等式，求出解集是解答本题的关键．解不等式应根据不等式的基本性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    11．在函数y=$\sqrt{x+4}$+x-2中，自变量x的取值范围是x≥-4且x≠0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．如图，点A、B、C在⊙O上，AC∥OB，∠BAO=25°，则∠BOC的度数为（　　）
    A．25°B．50°C．60°D．80°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

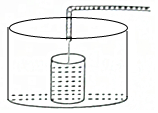    9．小明做了一个数学实验：将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内，看作一个容器．然后，小明对准玻璃杯口匀速注水，如图所示，在注水过程中，杯底始终紧贴鱼缸底部，则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是（　　）
    A．B．C．D．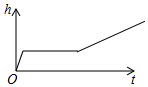

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图1，经过原点O的抛物线y=ax2+bx（a≠0）与x轴交于另一点A（$\frac{3}{2}$，0），在第一象限内与直线y=x交于点B（2，t）．
    （1）求这条抛物线的表达式；
    （2）在第四象限内的抛物线上有一点C，满足以B，O，C为顶点的三角形的面积为2，求点C的坐标；
    （3）如图2，若点M在这条抛物线上，且∠MBO=∠ABO，在（2）的条件下，是否存在点P，使得△POC∽△MOB？若存在，求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．一个正多边形的一个外角为30°，则它的内角和为1800°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

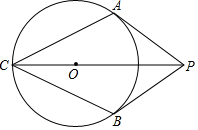    13．如图，PA、PB是⊙O的切线，A、B为切点，∠APB=60°，连接PO并延长与⊙O交于C点，连接AC，BC．
    （1）求证：四边形ACBP是菱形；
    （2）若⊙O半径为1，求菱形ACBP的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

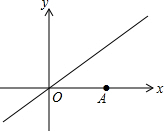    17．如图，点A坐标为（2，0），在直线y=$\frac{\sqrt{3}}{3}$x上取点M，使△AOM为等腰三角形，则满足条件的M坐标为（-$\sqrt{3}$，-1），（$\sqrt{3}$，1），（3，$\sqrt{3}$），（1，$\frac{\sqrt{3}}{3}$）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．已知一次函数y=kx+b的图象经过点（-2，-4），与正比例函数y=$\frac{1}{2}x$的图象交于点（4，a），求：
    （1）a的值；
    （2）k，b的值．

    查看答案和解析>>

    同步练习册答案