
【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( ) 
A.3:4
B.![]() :2
:2 ![]()
C.![]() :2
:2 ![]()
D.2 ![]() :
: ![]()
【答案】D
【解析】解:连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M, ∵根据三角形的面积和平行四边形的面积得:S△DEC=S△DFA= ![]() S平行四边形ABCD ,
S平行四边形ABCD ,
即 ![]() AF×DP=
AF×DP= ![]() CE×DQ,
CE×DQ,
∴AF×DP=CE×DQ,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠DAB=60°,
∴∠CBN=∠DAB=60°,
∴∠BFN=∠MCB=30°,
∵AB:BC=3:2,
∴设AB=3a,BC=2a,
∵AE:EB=1:2,F是BC的中点,
∴BF=a,BE=2a,
BN= ![]() a,BM=a,
a,BM=a,
由勾股定理得:FN= ![]() a,CM=
a,CM= ![]() a,
a,
AF= ![]() =
= ![]() a,
a,
CE= ![]() =2
=2 ![]() a,
a,
∴ ![]() aDP=2
aDP=2 ![]() aDQ
aDQ
∴DP:DQ=2 ![]() :
: ![]() .
.
故选:D.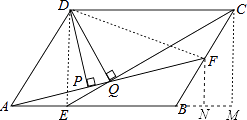
连接DE、DF,过F作FN⊥AB于N,过C作CM⊥AB于M,根据三角形的面积和平行四边形的面积得出S△DEC=S△DFA= ![]() S平行四边形ABCD , 求出AF×DP=CE×DQ,设AB=3a,BC=2a,则BF=a,BE=2a,BN=
S平行四边形ABCD , 求出AF×DP=CE×DQ,设AB=3a,BC=2a,则BF=a,BE=2a,BN= ![]() a,BM=a,FN=
a,BM=a,FN= ![]() a,CM=
a,CM= ![]() a,求出AF=
a,求出AF= ![]() a,CE=2
a,CE=2 ![]() a,代入求出即可.
a,代入求出即可.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度. 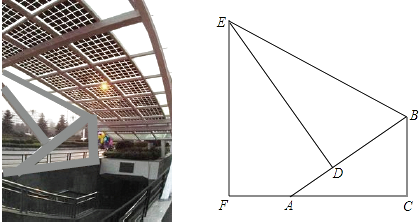
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
甲(kg) | 乙(kg) | 件数(件) | |
A | 5x | x | |
B | 4(40﹣x) | 40﹣x |
(2)安排生产A、B两种产品的件数有几种方案?试说明理由;
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面给出的正多边形的边长都是20cm,请分别按下列要求设计一种剪拼方法(用虚线表示你的设计方案,把剪拼线段用粗黑实线,在图中标注出必要的符号和数据,并作简要说明. 
(1)将图1中的正方形纸片剪拼成一个底面是正方形的直四棱柱模型,使它的表面积与原正方形面积相等;
(2)将图2中的正三角形纸片剪拼成一个底面是正三角形的直三棱柱模型,使它的表面积与原正三角形的面积相等;
(3)将图3中的正五边形纸片剪拼成一个底面是正五边形的直五棱柱模型,使它的表面积与原正五边形的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王大爷家有一块梯形形状土地,如图,AD∥BC , 对角线AD , BC相交于点O , 王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( ).
A.1:14
B.3:14
C.1:16
D.3:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com