
| 球的颜色 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东日照卷)数学 题型:解答题
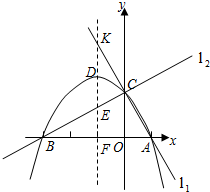
(2011•衢州)已知两直线l1,l2分别经过点A(1,0),点B(﹣3,0),并且当两直线同时相交于y正半轴的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l2交于点K,如图所示.
(1)求点C的坐标,并求出抛物线的函数解析式;
(2)抛物线的对称轴被直线l1,抛物线,直线l2和x轴依次截得三条线段,问这三条线段有何数量关系?请说明理由;
(3)当直线l2绕点C旋转时,与抛物线的另一个交点为M,请找出使△MCK为等腰三角形的点M,简述理由,并写出点M的坐标.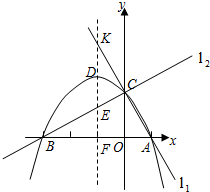
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东烟台卷)数学 题型:解答题
(2011•衢州)研究问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验,摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
活动结果:摸球实验活动一共做了50次,统计结果如下表:
| 球的颜色 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com