
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴的正半轴上,且OA=4,OC=3,若抛物线经过O,A两点,且顶点在BC边上,对称轴交BE于点F,点D,E的坐标分别为(3,0),(0,1).
(1)求抛物线的解析式;
(2)猜想△EDB的形状并加以证明;
(3)点M在对称轴右侧的抛物线上,点N在x轴上,请问是否存在以点A,F,M,N为顶点的四边形是平行四边形?若存在,请求出所有符合条件的点M的坐标;若不存在,请说明理由.

【答案】(1)y=﹣![]() x2+3x;(2)△EDB为等腰直角三角形;证明见解析;(3)(
x2+3x;(2)△EDB为等腰直角三角形;证明见解析;(3)(![]() ,2)或(
,2)或(![]() ,﹣2).
,﹣2).
【解析】试题分析:(1)由条件可求得抛物线的顶点坐标及A点坐标,利用待定系数法可求得抛物线解析式;
(2)由B、D、E的坐标可分别求得DE、BD和BE的长,再利用勾股定理的逆定理可进行判断;
(3)由B、E的坐标可先求得直线BE的解析式,则可求得F点的坐标,当AF为边时,则有FM∥AN且FM=AN,则可求得M点的纵坐标,代入抛物线解析式可求得M点坐标;当AF为对角线时,由A、F的坐标可求得平行四边形的对称中心,可设出M点坐标,则可表示出N点坐标,再由N点在x轴上可得到关于M点坐标的方程,可求得M点坐标.
解:(1)在矩形OABC中,OA=4,OC=3,
∴A(4,0),C(0,3),
∵抛物线经过O、A两点,
∴抛物线顶点坐标为(2,3),
∴可设抛物线解析式为y=a(x﹣2)2+3,
把A点坐标代入可得0=a(4﹣2)2+3,解得a=﹣![]() ,
,
∴抛物线解析式为y=﹣![]() (x﹣2)2+3,即y=﹣
(x﹣2)2+3,即y=﹣![]() x2+3x;
x2+3x;
(2)△EDB为等腰直角三角形.
证明:
由(1)可知B(4,3),且D(3,0),E(0,1),
∴DE2=32+12=10,BD2=(4﹣3)2+32=10,BE2=42+(3﹣1)2=20,
∴DE2+BD2=BE2,且DE=BD,
∴△EDB为等腰直角三角形;
(3)存在.理由如下:
设直线BE解析式为y=kx+b,
把B、E坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线BE解析式为y=![]() x+1,
x+1,
当x=2时,y=2,
∴F(2,2),
①当AF为平行四边形的一边时,则M到x轴的距离与F到x轴的距离相等,即M到x轴的距离为2,
∴点M的纵坐标为2或﹣2,
在y=﹣![]() x2+3x中,令y=2可得2=﹣
x2+3x中,令y=2可得2=﹣![]() x2+3x,解得x=
x2+3x,解得x=![]() ,
,
∵点M在抛物线对称轴右侧,
∴x>2,
∴x=![]() ,
,
∴M点坐标为(![]() ,2);
,2);
在y=﹣![]() x2+3x中,令y=﹣2可得﹣2=﹣
x2+3x中,令y=﹣2可得﹣2=﹣![]() x2+3x,解得x=
x2+3x,解得x=![]() ,
,
∵点M在抛物线对称轴右侧,
∴x>2,
∴x=![]() ,
,
∴M点坐标为(![]() ,﹣2);
,﹣2);
②当AF为平行四边形的对角线时,
∵A(4,0),F(2,2),
∴线段AF的中点为(3,1),即平行四边形的对称中心为(3,1),
设M(t,﹣![]() t2+3t),N(x,0),
t2+3t),N(x,0),
则﹣![]() t2+3t=2,解得t=
t2+3t=2,解得t=![]() ,
,
∵点M在抛物线对称轴右侧,
∴x>2,
∵t>2,
∴t=![]() ,
,
∴M点坐标为(![]() ,2);
,2);
综上可知存在满足条件的点M,其坐标为(![]() ,2)或(
,2)或(![]() ,﹣2).
,﹣2).


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】近几年,移动电商发展迅速,以下是2017年某调查机构发布的相关的统计表和统计图的一部分。请根据以上信息解答下列问题:

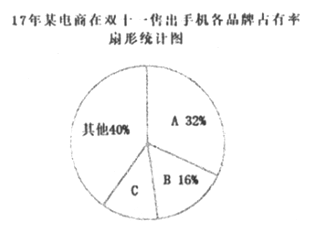
(1)2017年10月“移动电商行业用户规模”是___________亿台(结果精确到0.1亿台);并补全条形统计图;
(2)2017年10—12这三个月“移动电商行业用户规模”比上个月增长台数的平均数为___________亿台,若按此平均数增长,请你估计2018年1月“移动电商行业用户规模”为___________亿台(结果精确到0.1亿台);
(3)2017年某电商在双十一共售出手机12000台,则C品牌手机售出的台数是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)+3+(-5)
(2)-89-11
(3)(﹣5.5)+(﹣3.2)﹣(﹣2.5)﹣4.8
(4)17﹣(﹣8)×(﹣2)+4×(﹣3)
(5)(-32![]() )-[5
)-[5![]() -(+3
-(+3![]() )+(-5
)+(-5![]() )+(-2
)+(-2![]() )]
)]
(6)(![]() )×(﹣12)
)×(﹣12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,四边形ABCD是正方形,点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:DEBF=EF;
(2)若点G为CB延长线上一点,其余条件不变。请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明);

查看答案和解析>>
科目:初中数学 来源: 题型:
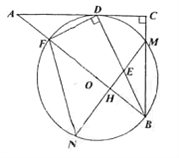
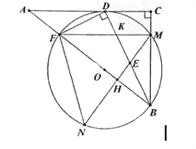
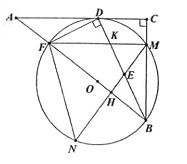
【题目】如图,在Rt△ABC中,∠C=90°,D为AC上一点,连接BD,DF⊥BD交AB于点F,△BDF的外接圆⊙O与边BC相较于点M,与AC相切于点D。过点M作AB的垂线交BD于点E,交⊙O于点N,交AB于点H,连接FN.
(1)求证:BD平分∠ABC;
(2)连接FM与BD相交于点K,求证:MK=ME;
(3)若AF=1,tan∠N=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花果山是旅游胜地,据统计2014年9月30日花果山旅游人数为2万人, 十· 一黄金周期间,花果山7天中每天旅游人数的变化情况如下表(正数表示比9月30日多的人数,负数表示比9月30日少的人数):
![]()
(1)请判断7天内游客人数量最多和最少的各是哪一天?它们相差多少万人?
(2)求这7天去花果山旅游的总人数.
(3)如果去花果山旅游平均每人消费300元,求风景区在此7天内的总收入.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3 cm,动点M自点A出发沿AB方向以1 cm/s的速度运动,同时点N自D点出发沿折线DC—CB以2 cm/s的速度运动,到达点B时运动同时停止,设△AMN的面积为y(单位:cm2),运动时间为x(单位:s),则下列图象中能大致反映y与x之间函数关系的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,开口向上的抛物线与![]() 轴交于
轴交于![]() 两点,
两点, ![]() 为抛物线的顶点,
为抛物线的顶点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() . 若
. 若![]() 的长分别是方程
的长分别是方程![]() 的两根,且
的两根,且![]()
(1)求抛物线对应的二次函数解析式和点![]() 的坐标。
的坐标。
(2)若点M为x轴正半轴上一个动点,N为线段AC上的一个动点,连接MN、CM,是否存在这样的点M,使△AMN为直角三角形和△CMN为等腰三角形同时成立,如果存在,请求出所有符合条件的点M的坐标,如果不存在,请说明理由。
(3如图2,过点![]() 任作直线
任作直线![]() 交线段
交线段![]() 于点
于点![]() 求
求![]() 到直线
到直线![]() 的距离分别为
的距离分别为![]() ,请直接写出
,请直接写出![]() 的最大值.
的最大值.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com