
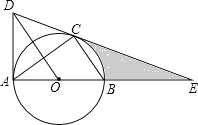
【题目】如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE=2![]() ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)连结OC,如图,先根据切线的性质得∠BAD=90°,再根据平行线的性质,由OD∥BC得∠1=∠3,∠2=∠4,加上∠3=∠4,则∠1=∠2,接着证明△AOD≌△COD,得到∠OCD=∠OAD=90°,于是可根据切线的判定定理得到DE是⊙O的切线;
(2)设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中利用勾股定理得到r2+(2![]() )2=(6﹣r)2,解得r=2,再利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
)2=(6﹣r)2,解得r=2,再利用正切函数求出∠COE=60°,然后根据扇形面积公式和S阴影部分=S△COE﹣S扇形BOC进行计算即可.
解:(1)连结OC,如图,∵AD为⊙O的切线,∴AD⊥AB,∴∠BAD=90°,
∵OD∥BC,∴∠1=∠3,∠2=∠4,∵OB=OC,∴∠3=∠4,∴∠1=∠2,
在△OCD和△OAD中,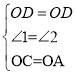 ,
,
∴△AOD≌△COD(SAS);
∴∠OCD=∠OAD=90°,
∴OC⊥DE,
∴DE是⊙O的切线;
(2)设半径为r,则OE=AE﹣OA=6﹣r,OC=r,在Rt△OCE中,∵OC2+CE2=OE2,
∴r2+(2![]() )2=(6﹣r)2,解得r=2,∵tan∠COE=
)2=(6﹣r)2,解得r=2,∵tan∠COE=![]() =
=![]() =
=![]() ,
,
∴∠COE=60°,
∴S阴影部分=S△COE﹣S扇形BOC=![]() ×2×2
×2×2![]() ﹣
﹣![]()
=2![]() ﹣
﹣![]() π.
π.



 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两个小孔形状、大小都相同,正常水位时,大孔水面常度AB=20米,顶点M距水面6米(即MO=6米),小孔水面宽度BC=6米,顶点N距水面4.5米.航管部门设定警戒水位为正常水位上方2米处借助于图中的平面直角坐标系解答下列问题:
(1)在汛期期间的某天,水位正好达到警戒水位,有一艘顶部高出水面3米,顶部宽4米的巡逻船要路过此处,请问该巡逻船能否安全通过大孔?并说明理由.
(2)在问题(1)中,同时桥对面又有一艘小船准备从小孔迎面通过,小船的船顶高出水面1.5米,顶部宽3米,请问小船能否安全通过小孔?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随州市新水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD.
(1)求最短的斜拉索DE的长;
(2)求最长的斜拉索AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式﹣利用函数图象研究其性质﹣应用函数解决问题”的学习过程.在画函数图象时,我们通过描点或平移的方法画出了一个陌生函数的大致图象,结合上面经历的学习过程,现在来解决下面问题:在函数y=![]() 中,当x=0时,y=1;当x=2时,y=
中,当x=0时,y=1;当x=2时,y=![]() .
.
(1)求这函数的表达式 ;
(2)在给出的平面直角坐标系中画出这个函数的大致图象并写出这个函数的一条性质 ;
(3)结合你所画的函数图象与y=![]() x+
x+![]() 的图象,直接写出不等式组
的图象,直接写出不等式组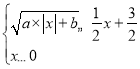 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A点坐标为(1,0),C点坐标为(7,0),若点P在直线y=kx+3上运动时,只存在一个点P使∠APC=90°,则k的值是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②a﹣b+c<0;③4a+b+c=0;④抛物线的顶点坐标为(2,b);⑤当x<1时,y随x增大而增大.其中结论正确的是( )
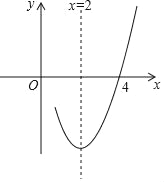
A. ①②③ B. ①④⑤ C. ①③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,将四边形ACBD沿直线EF折叠,使D与C重合,CE与CF分别交AB于点G、H.
(1)求证:△AEG∽△CHG;
(2)△AEG与△BHF是否相似,并说明理由;
(3)若BC=1,求cos∠CHG的值.
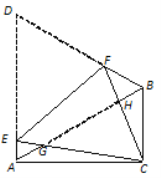
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有![]() ,
,![]() 为原点,
为原点,![]() ,
,![]() ,将此三角形绕点
,将此三角形绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,抛物线
,抛物线![]()
![]() 过
过![]() 三点.
三点.
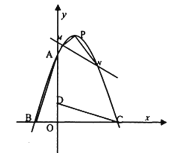
(1)求此抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)直线![]() 与抛物线交于
与抛物线交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值;
的值;
(3)抛物线的对称轴上是否存在一点![]() 使得
使得![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OAB中,∠AOB=100°,OA=12,C是OB的中点,CD⊥OB交![]() 于点D,以OC为半径的
于点D,以OC为半径的![]() 交OA于点E,则图中阴影部分的面积是( )
交OA于点E,则图中阴影部分的面积是( )
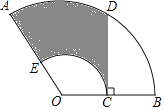
A. 12π+18![]() B. 12π+36
B. 12π+36![]() C. 6π+18
C. 6π+18![]() D. 6π+36
D. 6π+36![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com