
 ��ͼ����x=2ʱ��������y=ax2+bx+cȡ����Сֵ-1��������������y�ύ�ڵ�C��0��3������x�ύ�ڵ�A��B��
��ͼ����x=2ʱ��������y=ax2+bx+cȡ����Сֵ-1��������������y�ύ�ڵ�C��0��3������x�ύ�ڵ�A��B������ ��1���ɵ�x=2ʱ��������y=ax2+bx+cȡ����Сֵ-1���ɵ�������y=ax2+bx+c�Ķ�������Ϊ��2��-1�������ɵ�y=ax2+bx+c=a��x-2��2-1��������������y�ύ�ڵ�C��0��3����������������ߵĽ���ʽ��
��2����y1-y2=��x2-4x+3��-[��x+1��2-4��x+1��+3]=3-2x��Ȼ��ֱ����۵�xΪ��ֵʱ��y1��y2�Ĵ�С��
��3����������õ�A��B�����꣬�̶����ֱ��AC�Ľ���ʽ�������E������Ϊ����x��3-x�������F������Ϊ����x��x2-4x+3����������ô𰸣�
����EF��OC���ɵá�DEF=45�㣬���ڡ�DEF��ֻ���Ե�D��FΪֱ�Ƕ��㣬Ȼ��ֱ���⼴����ô𰸣�
��� �⣺��1���ߵ�x=2ʱ��������y=ax2+bx+cȡ����Сֵ-1��
��������y=ax2+bx+c�Ķ�������Ϊ����2��-1����
��y=ax2+bx+c=a��x-2��2-1��
����������y�ύ�ڵ�C��0��3����
��4a-1=3��
��ã�a=1��
�������ߵĽ���ʽΪ��y=��x-2��2-1=x2-4x+3��
��2����y1-y2=��x2-4x+3��-[��x+1��2-4��x+1��+3]=3-2x��
�൱3-2x��0����x��$\frac{3}{2}$ʱ��y1��y2��
��3-2x=0����x=$\frac{3}{2}$ʱ��y1=y2��
��3-2x��0����x��$\frac{3}{2}$ʱ��y1��y2��
��3���ٴ���x=$\frac{3}{2}$��ʹ�߶�EF���
��y=0����x2-4x+3=0��
��ã�x1=1��x2=3��
���A��3��0������B��1��0����
��ֱ��AC�Ľ���ʽΪ��y=mx+n��
��$\left\{\begin{array}{l}{n=3}\\{3m+n=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-1}\\{n=3}\end{array}\right.$��
��ֱ��AC�Ľ���ʽΪ��y=-x+3���߶�AC���е�D������Ϊ����$\frac{3}{2}$��$\frac{3}{2}$����
���E����������x��3-x�������F����������x��x2-4x+3����
��EF=��3-x��-��x2-4x+3��=-x2+3x=-��x-$\frac{3}{2}$��2+$\frac{9}{4}$��
�൱x=$\frac{3}{2}$ʱ��EF�����ֵΪ$\frac{9}{4}$��
�ڡ�EF��OC��
���DEF=45�㣬���ڡ�DEF��ֻ���Ե�D��FΪֱ�Ƕ��㣬
���Ե�FΪֱ�Ƕ��㣬��DF��EF����ʱ��DEF�ס�ACO��
��DF����ֱ��Ϊ��y=$\frac{3}{2}$��
��x2-4x+3=$\frac{3}{2}$����ã�x1=$\frac{4-\sqrt{10}}{2}$��x2=$\frac{4+\sqrt{10}}{2}$��3�����������⣬��ȥ����
��x=$\frac{4-\sqrt{10}}{2}$����y=-x+3���õ�E������Ϊ����$\frac{4-\sqrt{10}}{2}$��$\frac{2+\sqrt{10}}{2}$����
����DΪֱ�Ƕ��㣬��DF��AC����ʱ��DEF�ס�OCA��
�ߵ�DΪ�߶�AC���е㣬
��DF����ֱ�߹�ԭ��O�����ϵʽΪy=x��
��x2-4x+3=x��
��ã�x1=$\frac{5-\sqrt{13}}{2}$��x2=$\frac{5+\sqrt{13}}{2}$��3�����������⣬��ȥ����
��x=$\frac{5-\sqrt{13}}{2}$����y=-x+3���õ�E������Ϊ����$\frac{5-\sqrt{13}}{2}$��$\frac{1+\sqrt{13}}{2}$����
���� �������ڶ��κ������ۺ��⣬�����˴���ϵ���������Ľ���ʽ�����������ε��ж��������Լ����κ�������ֵ���⣮ע�ⷽ��˼�������ν��˼���Ӧ�ã�


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬��CD=BE��BD��CE�ཻ�ڵ�P��APƽ�֡�BAC����֤��AB=AC��
��ͼ����ABC�У�D��E�ֱ���AC��AB�ϵĵ㣬��CD=BE��BD��CE�ཻ�ڵ�P��APƽ�֡�BAC����֤��AB=AC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵȱߡ�ABC�У�MΪBC��������һ�㣨����B��C���㣩��PΪBC�ӳ�����һ�㣬N�ǡ�ACP��ƽ������һ�㣮��֪��AMN=60�㣬��֤��AM=NM��
��ͼ���ڵȱߡ�ABC�У�MΪBC��������һ�㣨����B��C���㣩��PΪBC�ӳ�����һ�㣬N�ǡ�ACP��ƽ������һ�㣮��֪��AMN=60�㣬��֤��AM=NM���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
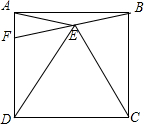 ��ͼ��E��������ABCD��һ�㣬��CDE�ǵȱ������Σ�����EB��EA���ӳ�BE��AD���ڵ�F�����AFB�Ķ����ǣ�������
��ͼ��E��������ABCD��һ�㣬��CDE�ǵȱ������Σ�����EB��EA���ӳ�BE��AD���ڵ�F�����AFB�Ķ����ǣ�������| A�� | 45�� | B�� | 60�� | C�� | 80�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
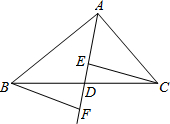 ��֪���⣺��ͼ���ڡ�ABC�У���D��BC�ĵ㣬������AD�����߶�AD�����ӳ����Ϸֱ�ȡ��E��F������CE��BF�����BDF�ա�CDF���ж����������������Ǽ����⣿����������⣬�����֤��������Ǽ����⣬������һ���ʵ����������������κθ����ߣ�ʹ����Ϊ�����⣮�������ӵ������ǣ�CE��BF��������֤����
��֪���⣺��ͼ���ڡ�ABC�У���D��BC�ĵ㣬������AD�����߶�AD�����ӳ����Ϸֱ�ȡ��E��F������CE��BF�����BDF�ա�CDF���ж����������������Ǽ����⣿����������⣬�����֤��������Ǽ����⣬������һ���ʵ����������������κθ����ߣ�ʹ����Ϊ�����⣮�������ӵ������ǣ�CE��BF��������֤�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com