
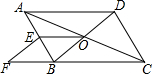
 如图,在?ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD
如图,在?ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD分析 (1)证明两组对边分别平行即可.
(2)结论:当AD⊥BD时,四边形OBFE是矩形.只要证明∠BOE=90°即可.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.只要证明OB=OE即可.
解答 (1)证明:四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB中点,
∴AE=BE
∴OE为△ABC的中位线,
∴OE∥BC,
∵EF∥BD,
∴四边形OBFE是平行四边形.
解:(2)结论:当AD⊥BD时,四边形OBFE是矩形
∵四边形ABCD是平行四边形,
∴OB=OD
∵E为AB中点,
∴AE=BE
∴OE为△ABD的中位线,
∴OE∥AD,
∴∠BOE=∠BDA,
∵AD⊥BD,
∴∠BOE=BDA=90°,
∵四边形OBFE是平行四边形,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.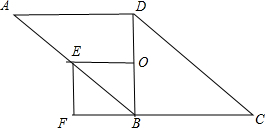
理由:∵OE为△ABD的中位线,
∴OE=$\frac{1}{2}$AD
∵O为BD中点,
∴OB=$\frac{1}{2}$BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
点评 本题考查平行四边形的性质、正方形的性质和判定、矩形的判定和性质、三角形的中位线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
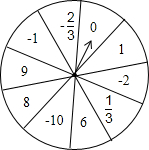 如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?
如图是芳芳设计的自由转动的转盘,上面写有10个有理数,想想看,转得下列各数的概率是多少?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
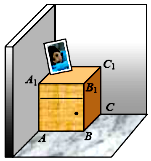 如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.
如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.当AB=4,BC=4,CC1=5时,则蚂蚁爬过的最短路径的长为$\sqrt{89}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
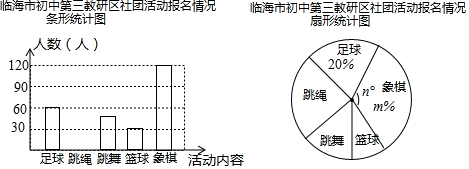
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
| 摸到白球的次数m | 63 | 124 | 178 | 302 | 481 | 599 | 1803 |
| 摸到白球的频率$\frac{m}{n}$ | 0.63 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com