
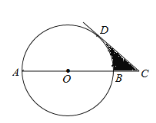
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD切⊙O于点D.若∠C =45°,AB=8.
(1)求BC的长;
(2)求阴影部分的面积(结果保留π).
【答案】(1)BC=![]() ;(2)
;(2)![]()
【解析】
(1)连接OD,由CD为圆O的切线,根据切线的性质得到OD与CD垂直,可得三角形OCD为直角三角形,同时由直径AB的长求出半径OC的长,根据锐角三角函数定义得到sinC为∠C的对边OD与斜边OC的比值,即可求出OC的长,则BC=OC-OB,可得出BC的长;
(2)由直角三角形中∠C的度数,根据直角三角形的两个锐角互余求出∠DOC的度数,求得CD的长度,利用直角三角形两直角边乘积的一半求出直角三角形COD的面积,利用扇形的面积公式求出扇形BOD的面积,用三角形COD的面积减去扇形COE的面积,即可求出阴影部分的面积.
(1)连接OD,
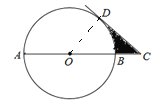
∵CD切⊙O于点D,
∴OD⊥CD,
∵AB=8,
∴OB=OD=![]() AB=4,
AB=4,
又在直角三角形OCD中,∠C=45°,
∴sinC=sin45°=![]() ,
,
即OC=![]() ,
,
∴BC=OC-OB=![]() ;
;
(2)∵∠OCD=90°,∠C=45°,
∴∠COD=45°,
∴CD=OD=4,
∴S△COD=![]() CD·OD=
CD·OD=![]() =8,
=8,
∴S扇形BOD=![]() =2π,
=2π,
则S阴影= S△COD - S扇形BOD =8-2π.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,与函数y=![]() x+b的图象交于点C(﹣2,m).
x+b的图象交于点C(﹣2,m).
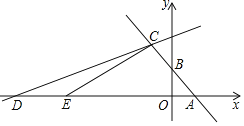
(1)求m和b的值;
(2)函数y=![]() x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
①当△ACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使△ACE为直角三角形?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.

(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线和反射点P3;
(2)当⊙O的半径为1时,如图3:
①第一象限内的一条入射光线平行于y轴,且自⊙O的外部照射在圆上点P处,此光线经⊙O反射后,反射光线与x轴平行,则反射光线与切线l的夹角为___________°;
②自点M(0,1)出发的入射光线,在⊙O内顺时针方向不断地反射.若第1个反射点是P1,第二个反射点是P2,以此类推,第8个反射点是P8恰好与点M重合,则第1个反射点P1的坐标为___________;
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织“优质课大赛”活动,经过评比有两名男教师和两名女教师获得一等奖,学校将从这四名教师中随机挑选两位教师参加市教育局组织的决赛,挑选的两位教师恰好是一男一女的概率为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡在推进村村通公路某项目建设中,计划修建公路15千米.已知甲队单独完成修建公路所需得时间是乙队得1.5倍,甲队每天比乙队少修0.5千米.
(1)求甲、乙两队单独完成修建公路各需多少天?
(2)已知甲队每天的工作费用是4000元,乙队每天的工作费用是5000元,若该工程由甲乙两队合作完成,且工程的总费用不超过52000元,求乙队至少要工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
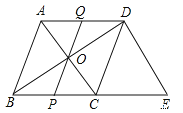
【题目】如图,在菱形ABCD中,对角线AC与BD相交于O点,AB=5,AC=6,过D点作DE//AC交BC的延长线于E点
(1)求△BDE的周长
(2)点P为线段BC上的点,连接PO并延长交AD于点Q,求证:BP=DQ
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com