
【题目】在![]() 中,若
中,若![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() 分别在
分别在![]() 和
和![]() 上,且
上,且![]() ,垂足为
,垂足为![]() ,
,![]() ,垂足为
,垂足为![]() (如图
(如图![]() ),则可以得到以下两个结论:
),则可以得到以下两个结论:
①![]() ;②
;②![]() .
.
那么在![]() 中,仍然有条件“
中,仍然有条件“![]() 是
是![]() 的角平分线,点
的角平分线,点![]() 和点
和点![]() ,分别在
,分别在![]() 和
和![]() 上”,请探究以下两个问题:
上”,请探究以下两个问题:
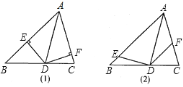
![]() 若
若![]() (如图
(如图![]() ),则
),则![]() 与
与![]() 是否仍相等?若仍相等,请证明;否则请举出反例.
是否仍相等?若仍相等,请证明;否则请举出反例.
![]() 若
若![]() ,则
,则![]() 是否成立?(只写出结论,不证明)
是否成立?(只写出结论,不证明)
【答案】(1)![]() 理由见解析,(2)不一定成立,理由见解析
理由见解析,(2)不一定成立,理由见解析
【解析】
(1)过点D作DM⊥AB于M,DN⊥AC于N,根据角平分线上的点到角的两边的距离相等可得DM=DN,再根据∠AED+∠AFD=180°,平角的定义得∠AFD+∠DFN=180°,可以推出∠DFN=∠AED,然后利用角角边定理证明△DME与△DNF全等,根据全等三角形对应边相等即可证明;
(2)不一定成立,若DE、DF在点D到角的两边的垂线段上或垂线段与点A的两侧,则成立,若是同侧则不成立.
![]() .
.
理由如下:
过点![]() 作
作![]() 于
于![]() ,
,![]() 于
于![]() ,
,
∵![]() 平分
平分![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
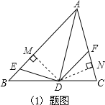
![]() 不一定成立.
不一定成立.
如图,若![]() 、
、![]() 在点
在点![]() 到角的两边的垂线段与顶点
到角的两边的垂线段与顶点![]() 的同侧则一定不成立,
的同侧则一定不成立,
经过![]() 的证明,若在垂线段上或两侧则成立,
的证明,若在垂线段上或两侧则成立,
所以不一定成立.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
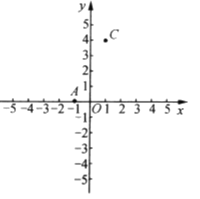
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
(1)求点![]() 的坐标,并画出
的坐标,并画出![]() ;
;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=AC=2cm,线段BC上一动点P从C点开始运动,到B点停止,以AP为边在AC的右侧作等边△APQ,则Q点运动的路径为cm. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在
,在![]() 中,
中,![]() 为
为![]() 边上的高,
边上的高,![]() 为
为![]() 的平分线,已知
的平分线,已知![]() ,
,![]()
![]() 求
求![]() 的度数;
的度数;
![]() 你发现
你发现![]() 与
与![]() 、
、![]() 之间有何关系?
之间有何关系?
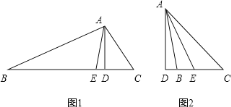
![]() 若将“题中的条件
若将“题中的条件![]() ”改为“
”改为“![]() ”如图
”如图![]() ,其它条件不变,则
,其它条件不变,则![]() 与
与![]() 、
、![]() 之间又有何关系?请说明理由.
之间又有何关系?请说明理由.
![]() 若将“题目中的条件
若将“题目中的条件![]() ,
,![]() ”改为“
”改为“![]() ,
,![]() ”,其它条件不变,求
”,其它条件不变,求![]() 、
、![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( ) 
A.2 ![]() π
π
B.![]() π
π
C.2π
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是⊙O的内接三角形,BC= ![]() .如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA=
.如图,若AC是⊙O的直径,∠BAC=60°,延长BA到点D,使得DA= ![]() BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由.
BA,过点D作直线l⊥BD,垂足为点D,请将图形补充完整,判断直线l和⊙O的位置关系并说明理由. 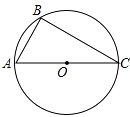
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com