练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．正方形具有而矩形不一定具有的性质是（　　）
    A．四个角都是直角B．四条边相等C．对角线相等D．对角线互相平分

    分析 根据正方形、矩形的性质，即可解答．

    解答 解：根据正方形和矩形的性质知，它们具有相同的特征有：四个角都是直角、对角线都相等、对角线互相平分，但矩形的长和宽不相等．
    故选：B．

    点评 本题考查了正方形和矩形的性质，解决本题的关键是熟记正方形和矩形的性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

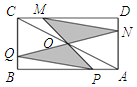    4．如图，矩形ABCD中，AB=4，BC=2，O为对角线AC的中点，点P、Q分别从A和B两点同时出发，在边AB和BC上匀速运动，并且同时到达终点B、C，连接PO、QO并延长分别与CD、DA交于点M、N．在整个运动过程中，图中阴影部分面积的大小变化情况是（　　）
    A．一直增大B．一直减小C．先减小后增大D．先增大后减小

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，在矩形ABCD中，点E，F，G，H分别是边AB，BC，CD，DA上的点，若∠1=∠2=∠3=∠4，则称四边形EFGH为矩形ABCD的反射四边形．
    （1）如图1，求证：反射四边形EFGH是平行四边形；
    （2）如图2，若AB=6，BC=8，求反射四边形EFGH的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

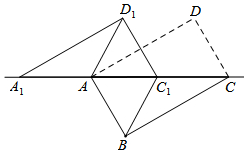    2．如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连结AD1，BC1，若∠ACB=30°，AB=1，CC1=x（0＜x＜2），△ACD与△A1C1D1重叠部分的面积为S，则下列结论：
    ①△A1AD1≌△CC1B；
    ②当x=1时，△BDD1为直角三角形；
    ③在平移过程中，四边形ABC1D1始终是平行四边形；
    ④S=$\frac{\sqrt{3}}{4}$（x-2）2（0＜x＜2）；
    其中正确的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．某商品四天内每天每斤的进价与售价信息如图所示，则售出这种商品每斤利润最大的是（　　）
    A．第一天B．第二天C．第三天D．第四天

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

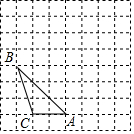    19．如图，方格纸中每一个小方格的边长为1个单位，试解答下列问题：
    （1）△ABC的顶点都在方格纸的格点上，先将△ABC向右平移2个单位，再向上平移3个单位，得到△A1B1C1，其中点A1、B1、C1分别是A、B、C的对应点，试画出
    △A1B1C1；
    （2）连接AA1、BB1，则线段AA1、BB1的位置关系为平行，线段AA1、BB1的数量关系为相等；
    （3）△A1B1C1的面积为3（平方单位）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列说法正确的是（　　）
    A．了解中央电视台新闻频道的收视率应采用全面调查
    B．了解岳池县初一年级学生的视力情况，现在我县城区甲、乙两所中学的初一年级随机地各抽取50名学生的视力情况
    C．反映岳池县6月份每天的最高气温的变化情况适合用折线统计图
    D．商家从一批粽子中抽取200个进行质量检测，200是总体

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

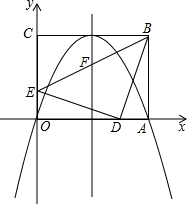    3．如图，在平面直角坐标系中，矩形OABC的顶点A，C分别在x轴，y轴的正半轴上，且OA=4，OC=3，若抛物线经过O，A两点，且顶点在BC边上，对称轴交BE于点F，点D，E的坐标分别为（3，0），（0，1）．
    （1）求抛物线的解析式；
    （2）猜想△EDB的形状并加以证明；
    （3）点M在对称轴右侧的抛物线上，点N在x轴上，请问是否存在以点A，F，M，N为顶点的四边形是平行四边形？若存在，请求出所有符合条件的点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．在平面直角坐标系中，直线l的关系式为：y=-x+4，x轴上方的点M到直线l的距离为$\sqrt{2}$且到x轴的距离为3，则点M的坐标为（3，3）．

    查看答案和解析>>

    同步练习册答案