
【题目】如图, Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F, (1)设AB=c, BC=a, AC=b, 求证: 内切圆半径r=![]() (a+b-c).
(a+b-c).
(2) 若AD交圆于P, PC交圆于H, FH//BC, 求∠CPD;
(3)若r=3![]() , PD=18, PC=27
, PD=18, PC=27![]() . 求△ABC各边长.
. 求△ABC各边长.
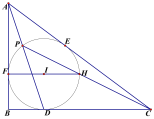
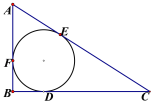
【答案】(1)证明见解析(2)45°(3)![]()
【解析】
(1)根据切线长定理,有AE=AF,BD=BF,CD=CE.易证四边形BDOF为正方形,BD=BF=r,用r表示AF、AE、CD、CE,利用AE+CE=AC为等量关系列式.
(2)∠CPD为弧DH所对的圆周角,连接OD,易得弧DH所对的圆心角∠DOH=90°,所以∠CPD=45°.
(3)由PD=18和r=3![]() 联想到垂径定理基本图形,故过圆心O作PD的垂线OM,求得弦心距OM=3,进而得到∠MOD的正切值.延长DO得直径DG,易证PG∥OM,得到同位角∠G=∠MOD.又利用圆周角定理可证∠ADB=∠G,即得到∠ADB的正切值,进而求得AB.再设CE=CD=x,用x表示BC、AC,利用勾股定理列方程即求出x.
联想到垂径定理基本图形,故过圆心O作PD的垂线OM,求得弦心距OM=3,进而得到∠MOD的正切值.延长DO得直径DG,易证PG∥OM,得到同位角∠G=∠MOD.又利用圆周角定理可证∠ADB=∠G,即得到∠ADB的正切值,进而求得AB.再设CE=CD=x,用x表示BC、AC,利用勾股定理列方程即求出x.
解:(1)证明:设圆心为O,连接OD、OE、OF,
∵⊙O分别与BC、CA、AB相切于点D、E、F
∴OD⊥BC,OE⊥AC,OF⊥AB,AE=AF,BD=BF,CD=CE
∴∠B=∠ODB=∠OFB=90°
∴四边形BDOF是矩形
∵OD=OF=r
∴矩形BDOF是正方形
∴BD=BF=r
∴AE=AF=AB-BF=c-r,CE=CD=BC-BD=a-r
∵AE+CE=AC
∴c-r+a-r=b
整理得:r=![]() (a+b-c)
(a+b-c)
(2)取FH中点O,连接OD
∵FH∥BC
∴∠AFH=∠B=90°
∵AB与圆相切于点F,
∴FH为圆的直径,即O为圆心
∵FH∥BC
∴∠DOH=∠ODB=90°
∴∠CPD=![]() ∠DOH=45°
∠DOH=45°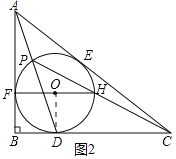
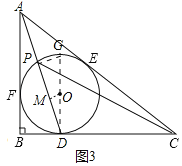
(3)设圆心为O,连接DO并延长交⊙O于点G,连接PG,过O作OM⊥PD于M
∴∠OMD=90°
∵PD=18
∴DM=![]() PD=9
PD=9
∵BF=BD=OD=r=3![]() ,
,
∴OM=![]() =
=![]() =
=![]() =3
=3
∴tan∠MOD=![]() =3
=3
∵DG为直径
∴∠DPG=90°
∴OM∥PG,∠G+∠ODM=90°
∴∠G=∠MOD
∵∠ODB=∠ADB+∠ODM=90°
∴∠ADB=∠G
∴∠ADB=∠MOD
∴tan∠ADB=![]() =tan∠MOD=3
=tan∠MOD=3
∴AB=3BD=3r=9![]()
∴AE=AF=AB-BF=9![]() 3
3![]() =6
=6![]()
设CE=CD=x,则BC=3![]() +x,AC=6
+x,AC=6![]() +x
+x
∵AB2+BC2=AC2
∴(9![]() )2.+(3
)2.+(3![]() +x)2=(6
+x)2=(6![]() +x)2
+x)2
解得:x=9![]()
∴BC=12![]() ,AC=15
,AC=15![]()
∴△ABC各边长AB=9![]() ,AC=15
,AC=15![]() ,BC=12
,BC=12![]()


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
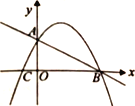
【题目】如图,直线![]() 交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
交坐标轴于A、B两点,直线AC⊥AB交x轴于点C,抛物线恰好过点A、B、C.
(1)求抛物线的表达式.
(2)当点M在线段AB上方的曲线上移动时,求四边形AOBM的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在网格中的位置如图所示(每个小正方形边长为1),AD⊥BC于D,下列选项中,错误的是( )

A. sinα=cosα B. tanC=2 C. sinβ=![]() D. tanα=1
D. tanα=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点P,Q分别在BC,AC上,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下面结论错误是( )
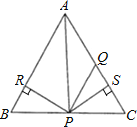
A. △BPR≌△QPSB. AS=ARC. QP∥ABD. ∠BAP=∠CAP
查看答案和解析>>
科目:初中数学 来源: 题型:
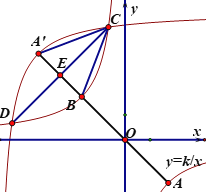
【题目】.如图,反比例函数y=k/x图像与直线y=-x交于A,B两点, 将双曲线右半支沿射线AB方向平移与左半支交于C,D. 点A到达A’点, A’B=BO, CE=6![]() . 则k=______.
. 则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
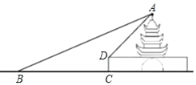
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
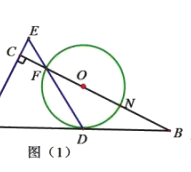
【题目】如图,![]() 中,
中,![]() ,以
,以![]() 上一点
上一点![]() 为圆心作圆与
为圆心作圆与![]() 切于点
切于点![]() ,与
,与![]() 分别交于点
分别交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() ;
;
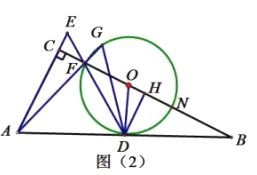
![]() 过点
过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
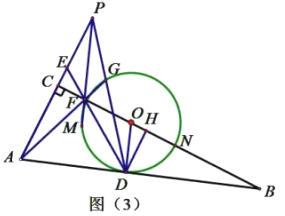
![]() 在
在![]() 的条件下,延长
的条件下,延长![]() 交
交![]() 的延长交于点
的延长交于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄河是中华民族的象征,被誉为母亲河,黄河壶口瀑布位于我省吉县城西45千米处,是黄河上最具气势的自然景观.其落差约30米,年平均流量1010立方米/秒.若以小时作时间单位,则其年平均流量可用科学记数法表示为( )

A. 6.06×104立方米/时 B. 3.136×106立方米/时
C. 3.636×106立方米/时 D. 36.36×105立方米/时
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com