
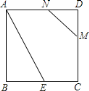
【题目】如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的端点M,N分别在CD,AD上滑动,当DM=______________时,△ABE与以D,M,N为顶点的三角形相似。
科目:初中数学 来源: 题型:
【题目】某超市销售糖果,将![]() 、
、![]() 、
、![]() 三种糖果搭配成甲、乙、丙三种礼盒方式销售,每个礼盒的成本分别为礼盒中
三种糖果搭配成甲、乙、丙三种礼盒方式销售,每个礼盒的成本分别为礼盒中![]() 、
、![]() 、
、![]() 糖果的成本之和,礼盒成本忽略不计.甲种礼盒每盒分别装有
糖果的成本之和,礼盒成本忽略不计.甲种礼盒每盒分别装有![]() 、
、![]() 、
、![]() 三种糖果
三种糖果![]() 、
、![]() 、
、![]() ,乙种礼盒每盒分别装有
,乙种礼盒每盒分别装有![]() 、
、![]() 、
、![]() 三种糖果
三种糖果![]() 、
、![]() 、
、![]() ,每盒甲的成本是每千克
,每盒甲的成本是每千克![]() 成本的12倍,每盒甲的销售利润率为25%,每盒甲的售价比每盒乙的售价低
成本的12倍,每盒甲的销售利润率为25%,每盒甲的售价比每盒乙的售价低![]() ,丙每盒在成本上提高30%标价后打九折销售获利为每千克
,丙每盒在成本上提高30%标价后打九折销售获利为每千克![]() 成本的1.7倍,当销售甲、乙、丙三种礼盒的数量之比为
成本的1.7倍,当销售甲、乙、丙三种礼盒的数量之比为![]() 时,销售的总利润率为__________.(用百分数表示)
时,销售的总利润率为__________.(用百分数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
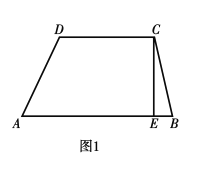
【题目】如图1,梯形![]() 中,上底
中,上底![]() 下底
下底![]() 高
高![]() 梯形的面积
梯形的面积![]() 动点
动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度匀速运动.
个单位长度的速度匀速运动.
![]() 请根据
请根据![]() 与
与![]() 的关系式,完成下列问题:
的关系式,完成下列问题:
|
|
|
|
| ··· | |
|
|
|
| ··· |
![]() 补充表格中的数据;
补充表格中的数据;
![]() 当
当![]() 时,表示的图形是_ .
时,表示的图形是_ .
![]() 梯形的面积
梯形的面积![]() 与
与![]() 的关系如图2所示,则点
的关系如图2所示,则点![]() 表示的实际意义是_ ;
表示的实际意义是_ ;

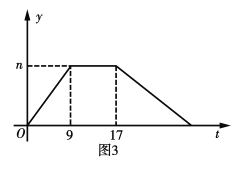
![]() 若点
若点![]() 运动的时间为
运动的时间为![]() 的面积为
的面积为![]() 与
与![]() 的关系如图3所示.求
的关系如图3所示.求![]() 的长和
的长和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠A=90°.
(1)请在图1中作出BC边上的中线(保留作图痕迹,不写作法);
(2)如图2,设BC边上的中线为AD,求证:BC=2AD.

查看答案和解析>>
科目:初中数学 来源: 题型:
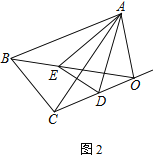
【题目】在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=30°,CD、BE交于点O,连接OA
(1) 如图1,求证:△ABE≌△ACD
(2) 如图1,求∠AOE的大小
(3) 当绕点A旋转至如图2所示位置时,若∠BAC=∠DAE=α,∠AOE=_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠1=∠2,点G为AD的中点,连接BG并延长,交AC于点E,F为AB上一点,且CF⊥AD于点H,下列判断中:①AD是△ABE的角平分线;②BE是△ABD边AD上的中线;③CH是△ACD边AD上的高.正确的个数有( )
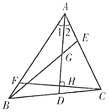
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC, ∠BAC=90°,D是斜边BC的中点,E,F分别是AB,AC边上的点,且DE⊥DF.
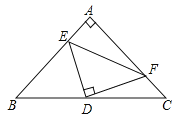
(1)判断DE和DF的数量关系,并说明理由;
(2)若BE=12,CF=5,求△DEF的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 地某厂和
地某厂和![]() 地某厂同时制成机器若干台,
地某厂同时制成机器若干台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,
台,![]() 地某厂可支援外地
地某厂可支援外地![]() 台,现决定给
台,现决定给![]() 地
地![]() 台,
台,![]() 地
地![]() 台,已知从
台,已知从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台,从
元每台,从![]() 运往
运往![]() 、
、![]() 两地的运费分别是
两地的运费分别是![]() 元每台、
元每台、![]() 元每台.
元每台.
(1)设![]() 地某厂运往
地某厂运往![]() 地
地![]() 台,求总运费为多少元?
台,求总运费为多少元?
(2)在(1)中,当![]() 时,总运费是多少元?
时,总运费是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com