
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 以上答案均不对 |
分析 先进行分式的混合运算,再解不等式组求其整数解为::-1、0、1、2,根据分式有意义的条件:所有的分母不为0,x≠±1,x≠0,则x=2,代入计算即可.
解答 解:M=($\frac{x}{x-1}$-$\frac{x}{{x}^{2}-1}$)÷$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$,
=$\frac{x(x+1)-x}{{x}^{2}-1}$•$\frac{(x-1)(x-1)}{x(x-1)}$,
=$\frac{{x}^{2}}{(x+1)(x-1)}$•$\frac{x-1}{x}$,
=$\frac{x}{x+1}$,
解不等式2x+4>0得:x>-2,
解不等式1-$\frac{x-1}{2}$>0得:x<3,
∴$\left\{\begin{array}{l}{2x+4>0}\\{1-\frac{x-1}{2}>0}\end{array}\right.$的解集为:-2<x<3,
它的整数解为:-1、0、1、2,
∵x2-1≠0,x≠0,
∴x≠±1,x≠0,
∴x=2,
当x=2时,M=$\frac{2}{2+1}$=$\frac{2}{3}$,
故选C.
点评 本题考查了分式的混合运算及一元一次不等式组的整数解,分式运算中,因式分解是基础,分子、分母中有公因式的要进行约分化为最简分式或整式.并注意运算律的应用;在解一元一次不等式组时,要排除分式中分母无意义的值.


 互动课堂系列答案
互动课堂系列答案科目:初中数学 来源: 题型:选择题
 如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )
如图,?ABCD中,E为AB中点,CE交BD于F,若△CBE的面积为S,则△DCF的面积为( )| A. | $\frac{2}{3}S$ | B. | S | C. | $\frac{4}{3}S$ | D. | 2S |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
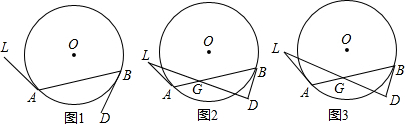
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O和⊙O′相交于A、B两点,过A点分别作两圆的切线交对方于D、C,连接DB并延长交⊙O于E,已知CO′=5,⊙O′的半径为4,则AE的长为( )
如图,⊙O和⊙O′相交于A、B两点,过A点分别作两圆的切线交对方于D、C,连接DB并延长交⊙O于E,已知CO′=5,⊙O′的半径为4,则AE的长为( )| A. | 3 | B. | 2$\sqrt{5}$ | C. | $\sqrt{21}$ | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com