
【题目】已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,对称轴是直线 ![]() .则下列结论中,正确的是( )
.则下列结论中,正确的是( ) 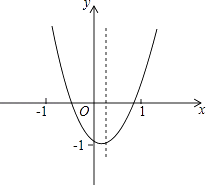
A.a<0
B.c<﹣1
C.a﹣b+c<0
D.2a+3b=0
【答案】D
【解析】解:A、∵二次函数的图象开口向上,
∴a>0,故本选项错误;
B、∵二次函数的图象与y轴的交点在点(0,﹣1)的上方,
∴c>﹣1,故本选项错误;
C、把x=﹣1代入y=ax2+bx+c得:y=a﹣b+c,
∵从二次函数的图象可知当x=﹣1时,y>0,
即a﹣b+c>0,故本选项错误;
D、∵二次函数的图象的对称轴是直线 ![]() ,
,
∴﹣ ![]() =
= ![]() ,
,
﹣3b=2a,
2a+3b=0,故本选项正确;
故选D.
【考点精析】关于本题考查的二次函数图象以及系数a、b、c的关系,需要了解二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能得出正确答案.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】在云南省某市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为:“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图. 
你结合图中信息,解答下列问题:
(1)本次共调查了名学生;
(2)被调查的学生中,最喜爱丁类图书的学生有人,最喜爱甲类图书的人数占本次被调查人数的%;扇形统计图中甲类部分的圆心是 .
(3)在最喜爱丙类图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生2400人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D交AC于点E,那么下列结论中正确的是 ( )
①△BDF和△CEF都是等腰三角形
②DE=BD+CE
③△ADE的周长等于AB和AC的和
④BF=CF

A. ①②③④ B. ①②③ C. ①② D. ①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E,F是对角线BD上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后,得到△ABQ,连接EQ,求证: 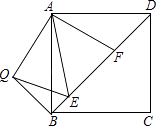
(1)EA是∠QED的平分线;
(2)EF2=BE2+DF2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O在坐标原点,顶点A在x轴上,∠B=120°,OA=2,将菱形OABC绕原点顺时针旋转105°至OA′B′C′的位置,则点B′的坐标为( ) 
A.( ![]() ,﹣
,﹣ ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(2,﹣2)
D.( ![]() ,﹣
,﹣ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,
,![]() 随
随![]() 增大而增大,它的图象经过点
增大而增大,它的图象经过点![]() 且与
且与![]() 轴的夹角为
轴的夹角为![]() ,
,
![]() 确定这个一次函数的解析式;
确定这个一次函数的解析式;
![]() 假设已知中的一次函数的图象沿
假设已知中的一次函数的图象沿![]() 轴平移两个单位,求平移以后的直线及直线与
轴平移两个单位,求平移以后的直线及直线与![]() 轴的交点坐标.
轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A.k> ![]()
B.k≥ ![]()
C.k> ![]() 且k≠1
且k≠1
D.k≥ ![]() 且k≠1
且k≠1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=x2﹣(m﹣2)x+m的图象过点(﹣1,15),设其图象与x轴交于点A,B(A在B的左侧),点C在图象上,且S△ABC=1,求:
(1)求m;
(2)求点A,点B的坐标;
(3)求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com